| MONOGRÁFICO: Una calculadora gráfica para la enseñanza de las matemáticas - La calculadora gráfica PL (v 1.0) |
 |
 |
 |
| SOFTWARE - Software educativo |
| Written by Luis González |
| Sunday, 29 July 2012 07:55 |
|
Page 5 of 6
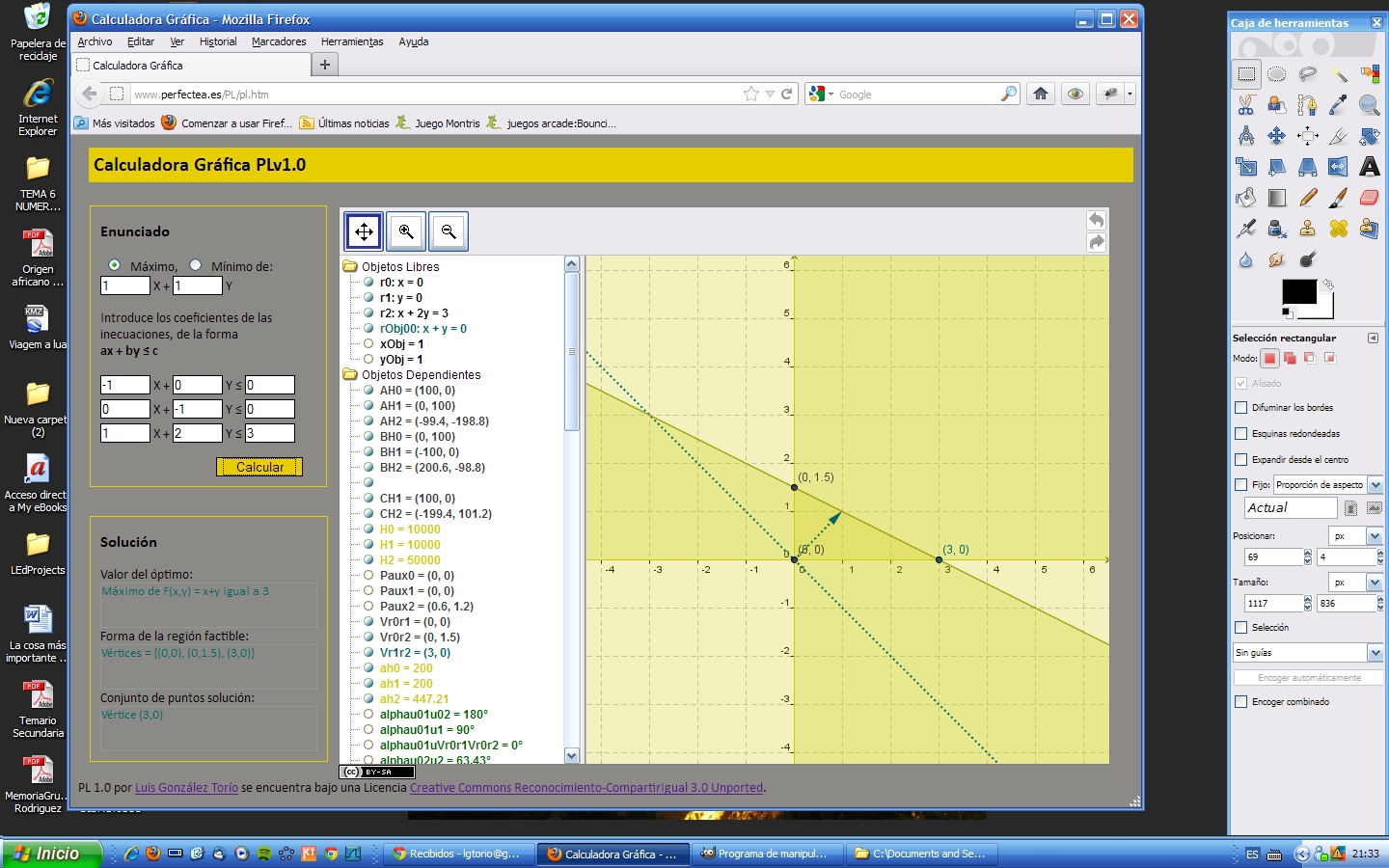
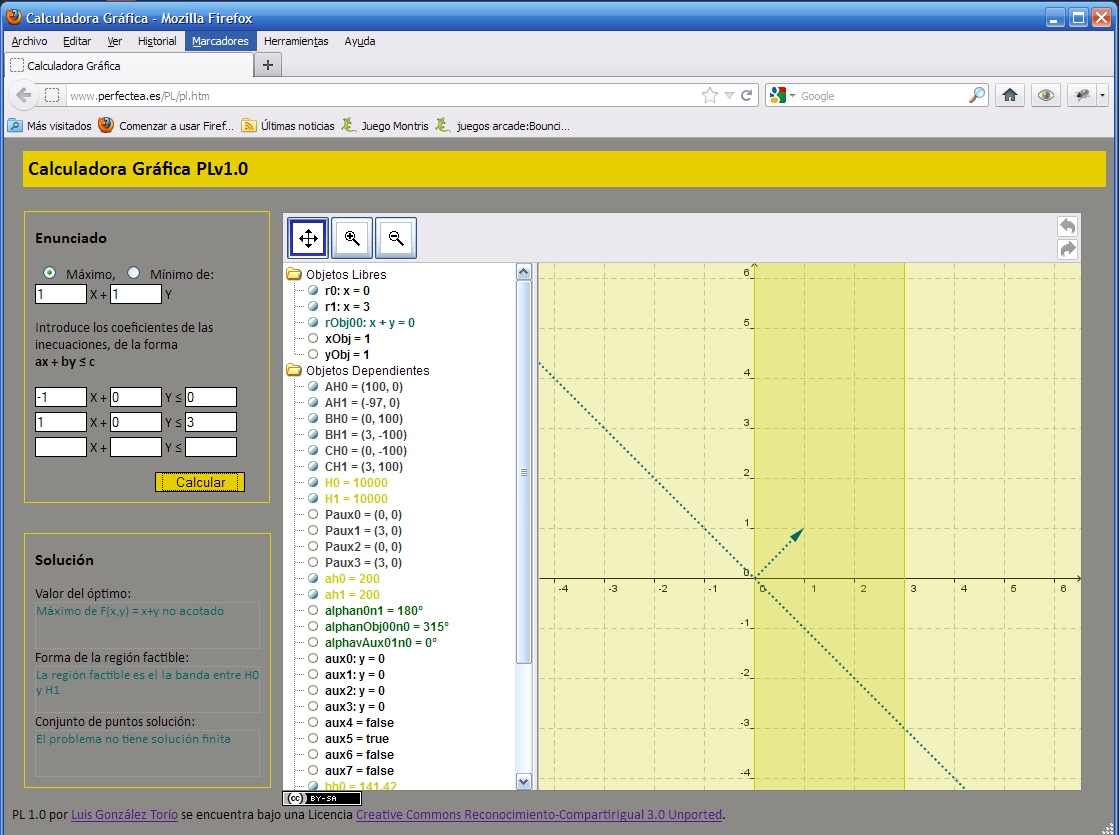
La calculadora gráfica PL (v 1.0)PL es un prototipo de calculadora gráfica y algebraica pensada para resolver problemas de programación lineal en dimensión 2. Está disponible en la siguiente dirección web: http://www.perfectea.es/PL/PL.htm y tiene licencia Creative Commons (Reconocimiento, Compartir igual). Su autor es el de este monográfico. El prototipo acepta regiones factibles definidas con un número de inecuaciones menor o igual a tres, y calcula el máximo o el mínimo de la correspondiente función objetivo gráficamente, detallando también las características de la región factible y el conjunto solución, cuando existe, tanto gráfica como analíticamente (explicitando las causas de la inexistencia de soluciones en cada caso correspondiente). Los siguientes ejemplos gráficos muestran distintos tipos de situaciones que, normalmente, quedan fuera del estudio que se hace en las aulas, debido a que la región factible presenta anomalías. (Y en todo caso, recomendamos utilizar la herramienta para comprobar posibilidades alternativas.)
Pantallazo - PL - region factible acotada unica solucion
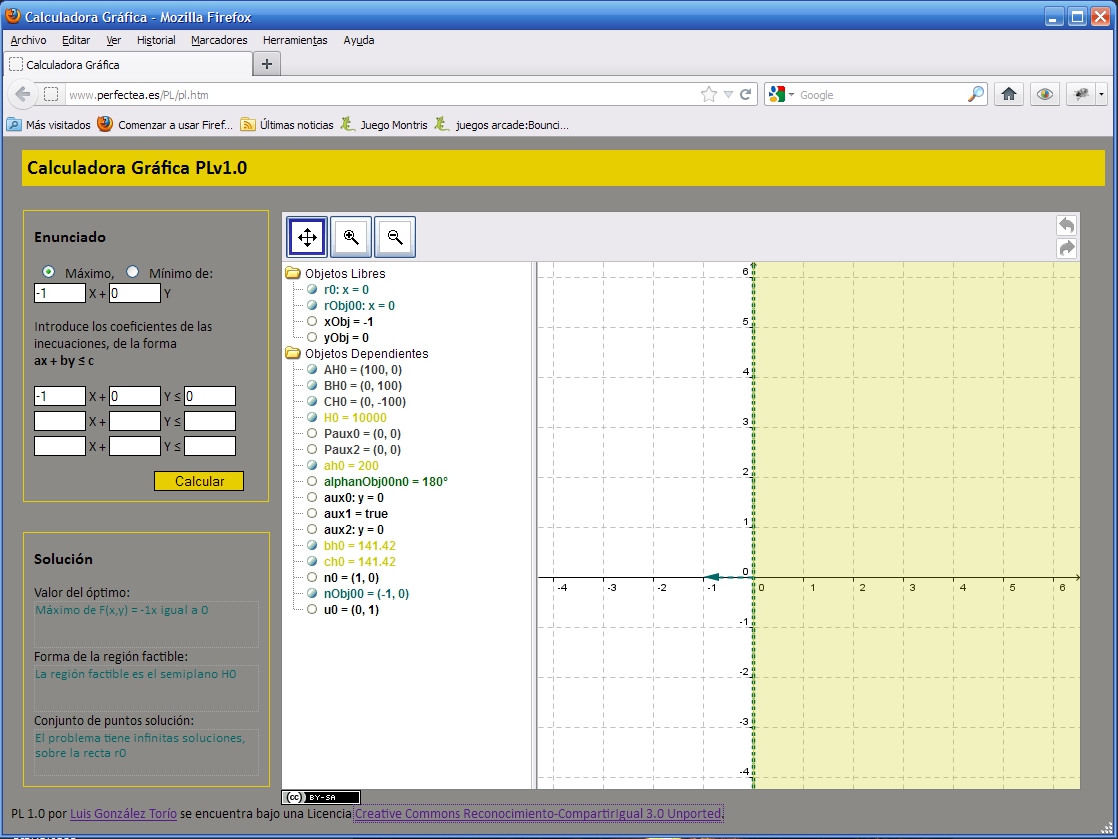
Pantallazo - PL - region factible no acotada infinitas soluciones
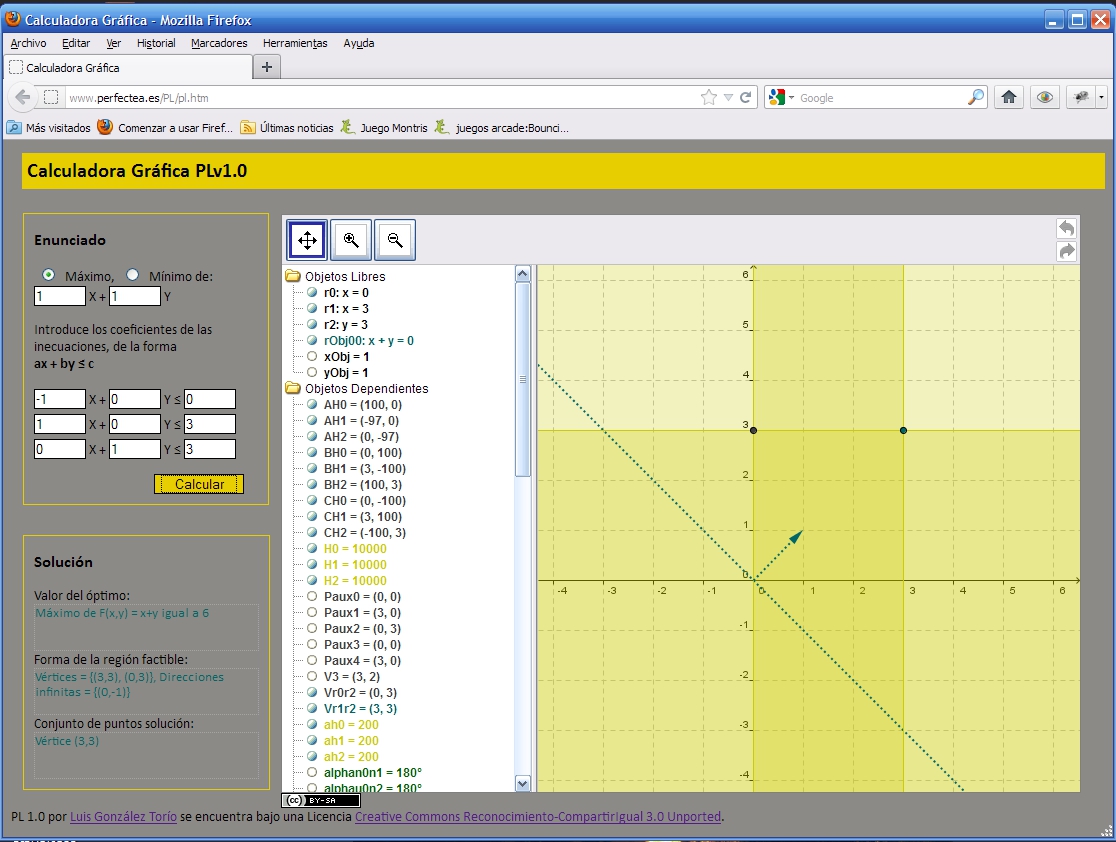
Pantallazo - PL - region factible no acotada unica solucion
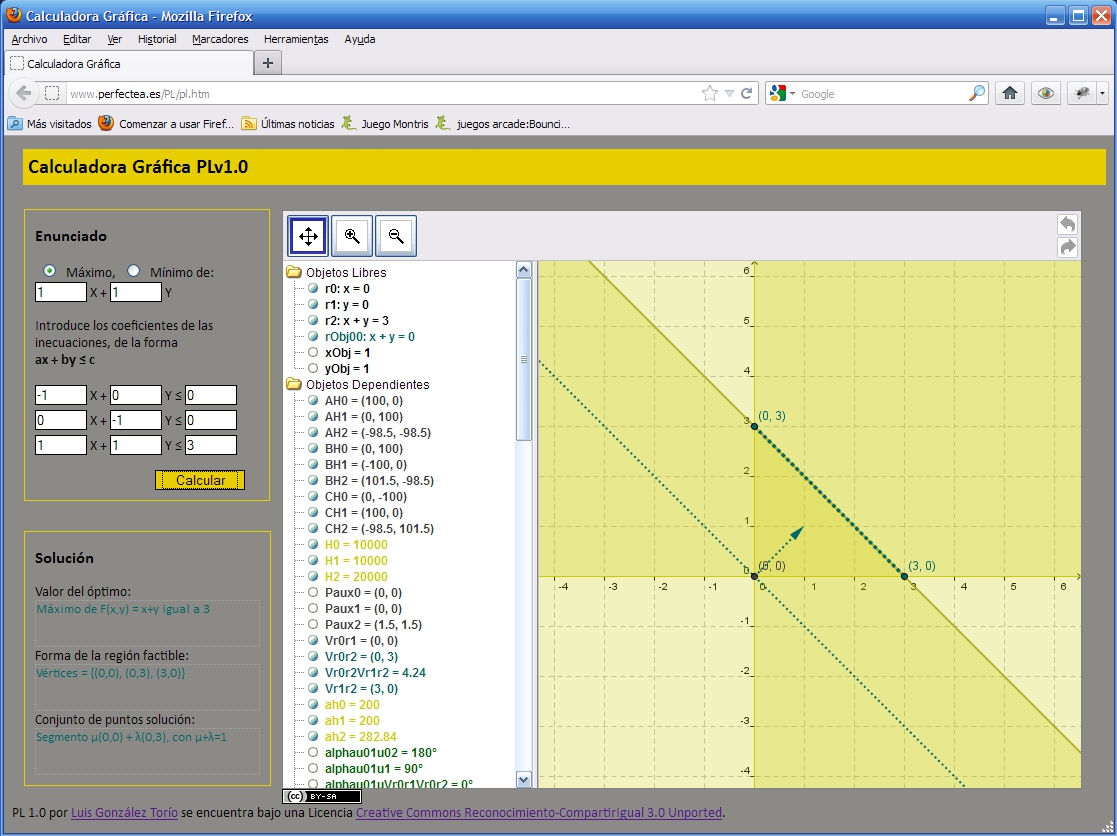
Pantallazo -PL - region factible acotada infinitas soluciones
Pantallazo -PL -region factible no acotada sin solucionj Está diseñado con una interfaz web, que consta fundamentalmente de 3 partes o “ventanas” bien definidas: una primera en la que se introducen los datos del problema a resolver (ventana “Enunciado”), una segunda ventana (ventana “Solución”) donde pueden leerse los datos relativos a la solución del problema, una vez que se ha calculado (óptimo, forma de la región factible y del conjunto de lo soluciones), y una tercera ventana gráfica, donde se muestra la representación gráfica de la solución (ver ilustración 1 del anexo). La ventana gráfica es una ventana abierta por un applet de Geogebra. De hecho, la solución construida por PL es lo que podría llamarse una “pseudoconstrucción” en Geogebra, en el sentido de que todos los cálculos matemáticos que realiza el programa están realizados utilizando Geogebra, aunque el algoritmo utilizado para encontrar la solución está programado en JavaScript. Como resultado, aunque la solución se obtiene mediante una construcción completamente realizada dentro del programa de geometría dinámica, no se garantiza que dicha solución sea resistente a variaciones dinámicas de los objetos libres que la definen, razón por la cual no se ha habilitado más interacción con la ventana gráfica que la necesaria para centrar, mediante movimiento de los ejes y cambio de escala, el dibujo que da lugar a la solución. Por supuesto, sería deseable una construcción de la solución tal que pudiera interactuarse gráficamente con la misma, aprovechando así todas las características propias del software de geometría dinámica. Dicha construcción es posible (y está realizada) si se restringe la forma de la región factible, aunque una única construcción resistente a cualquier variación de los objetos que definen la región factible ha sido imposible de obtener. Por consiguiente, si se desea utilizar la calculadora PL para trabajar la alternancia de registros analítico y gráfico, en el sentido del segundo al primero, debe ser utilizada estableciendo conjeturas acerca de qué inecuaciones definirán regiones con cierta forma que sean comprobadas después, o relegar directamente PL en favor de otro tipo de herramientas más adecuadas a este fin. |