Parámetros de dispersión. Son valores que informan de la concentración o dispersión de los datos respecto de los parámetros de centralización.

Por ejemplo, supongamos que hemos realizado el mismo examen en dos grupos distintos. En uno, todos los alumnos han sacado la misma nota, un 5; en otro, la mitad de los alumnos ha sacado un 0 y la otra mitad un 10. ¿Cuál es la media en los dos casos? ¿Se pueden considerar los dos grupos iguales si la media coincide?

Parece entonces que no es suficiente con las medidas de centralización, hace falta otros parámetros que informen sobre la mayor o menor concentración de los datos.

Los principales parámteros de dispersión son: el rango o recorrido, la desviación media, la varianza, la desviación típica y el coeficiente de variación.

Recorrido. Se define el recorrido como la diferencia entre el mayor y el menor de los valores de la variable. Se representa por R. Nos indica un intervalo en el que están comprendido todos los datos. Presenta el inconveniente de que sólo depende de los valores extremos, si uno se separa mucho el valor del rango aumenta excesivamente.

Desviación media. Al calcular la media, podemos ver la diferencia que hay entre este parámetro y cada valor de la variable, a la que llamaremos desviación. Podemos definir la desviación media como la media aritmética de todas las desviaciones, pero si la calculamos nos llevaremos la sorpresa de que vale 0. ¿Por qué?

Para evitar esta situación, se define la desviación media como la media aritmética de los valores absolutos de las desviaciones respecto de la media. La podremos calcular con la fórmula:

En la siguiente escena se puede calcular la desviación media.

Varianza. Se define la varianza como la media aritmética de los cuadrados de las desviaciones respecto de la media.

Para calcularla, aplicamos la fórmula:      

Si desarrollamos esta fórmula, podemos encontrar otra expresión más sencilla para el cálculo de la varianza: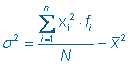

Desviación típica. Se define la desviación típica como la raíz cuadrada positiva de la varianza.

En la siguiente escena puedes calcular la varianza y la desviación típica para cualquier variable, tanto discreta como continua (utilizando las marcas de clase). La varianza se calcula utilizando las dos fórmulas para comprobar los resultados.

ACTIVIDADES

Actividad 1.

     Calcula en tu cuaderno la varianza y la desviación típica para el ejemplo del número de hermanos: 2, 3, 2, 3, 3, 3, 3, 4, 2, 2.

Una vez que las tienes en tu cuaderno, calcúlalas con la escena y compara los resultados.

Actividad 2.

     Calcula ahora la varianza y la desviación típica para el ejemplo de la estatura: 1.59, 1.75, 1.71, 1.85, 1.64, 1.62, 1.66, 1.60, 1.63, 1.76, utilizando los mismos intervalos que hayas construido antes.

Una vez que las tienes en tu cuaderno, calcúlalas con la escena y compara los resultados.

Actividad 3.

     Calcula la varianza (utilizando únicamente una fórmula) y la desviación típica en los ejercicios 1, 3, 5, 7 y 9 de la página de ejercicios.

COEFICIENTE DE VARIACIÓN.