Funciones racionales
Las funciones racionales son aquellas funciones que se obtienen de un cociente de polinomios:
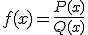 , siendo el grado de
, siendo el grado de 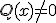
Un caso particular son las funciones del tipo 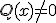 , donde k
, donde k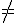 0 y n es un número natural.
0 y n es un número natural.
Con ayuda de la aplicación vamos a estudiar la representación gráfica de estas funciones.
Moviendo el deslizador del valor de n, puedes variar el exponente del denominador.
Moviendo el deslizador del valor k puedes cambiar la constante de proporcionalidad.
En la barra de herramientas puedes
desplazar los ejes ![]() , hacer
zoom para acercar
, hacer
zoom para acercar ![]() o para alejar
o para alejar ![]() la vista gráfica.
la vista gráfica.
Para calcular f(x0), la imagen del valor x0, desplaza el punto amarillo sobre el eje de abcisas.
La barra de Entrada te permite introducir el valor exacto del exponente y de la constante de proporcionalidad. Para ello, lo único que debes hacer es escribir, por ejemplo n=3 y presionar la tecla “intro”
Copia el dibujo en tu cuaderno para cada uno de los ejercicios.
1. Representa
gráficamente la función 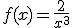
a. Calcula las asíntotas.
b. Estudia los intervalos de crecimiento y decrecimiento.
2. Representa
gráficamente la función 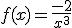
a. Calcula las asíntotas.
b. Estudia los intervalos de crecimiento y decrecimiento.
3. Representa
gráficamente la función 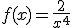
a. Calcula las asíntotas.
b. Estudia los intervalos de crecimiento y decrecimiento.
4. Representa
gráficamente la función 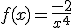
a. Calcula las asíntotas.
b. Estudia los intervalos de crecimiento y decrecimiento.
5. Cómo será
la gráfica de la función 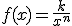 , sabiendo que k>0 y n
es impar.
, sabiendo que k>0 y n
es impar.
6. Cómo será
la gráfica de la función 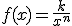 , sabiendo que k>0 y n
es par.
, sabiendo que k>0 y n
es par.
7. Cómo será
la gráfica de la función 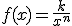 según el valor de k sea positivo o negativo y
el valor de n sea par o impar
según el valor de k sea positivo o negativo y
el valor de n sea par o impar

Esta obra está bajo una licencia de Creative Commons.