Función exponencial
Enunciado
Las funciones exponenciales son funciones del tipo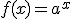 
, para a≥0 y a≠1.
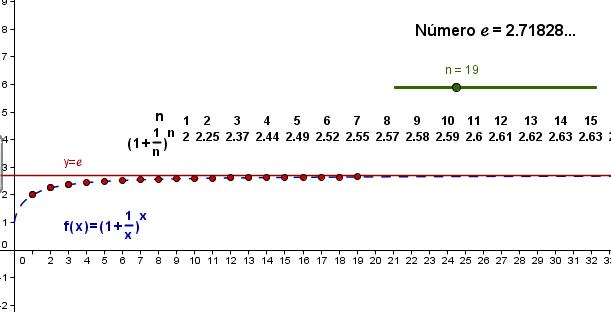
Una función exponencial muy utilizada es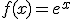 
(x), siendo e=2,718271...
Recuerda que el número e se obtiene del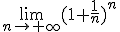 
.
Estas funciones aparecen habitualmente al describir procesos demográficos, económicos, biológicos,...
Qué hacer
Mueve el punto A para ver los valores que toma la función exponencial para cada valor de x.
En la barra de herramientas puedes
desplazar los ejes 
, hacer
zoom para acercar 
o para alejar 
la vista gráfica.
Mueve el deslizador verde del valor de "a" para cambiar la base de la función exponencial.
Activa la casilla de verificación de la función inversa, para representar la función inversa de la función exponencial.
Para volver a la posición inicial
haz clic en 
Preguntas
1. Representa en tu cuaderno sobre el mismo eje de coordenadas las funciones:
a.
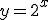
b.
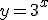
c.
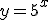
d.
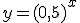
2. Describe las propiedades principales
de la función de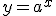 
para a>1, y para 0<a<1.
3. ¿Qué función se obtiene para a=1?. Explica por qué.
4. Se puede representar la función para un valor de a negativo. Explica por qué.
5. ¿Qué pasa para a=0? Justifica tu respuesta.
Esta obra está bajo una licencia de Creative Commons.