TEOREMAS DA ALTURA E DO CATETO
Xeometría
 
9. PROXECCIÓNS
Dado un punto P e unha recta r, chámase proxección do punto P sobre a recta r ao punto P', pé da perpendicular trazada dende P a r. Proxección do segmento AB é o segmento A'B' cuxos extremos son as proxeccións dos extremos A e B. 
Esta unidad interactiva requiere la máquina virtual de Java J2RE.
Na escena Descartes cambia a orientación e o tamaño do segmento AB movendo os puntos de control A e B.

9.1- Calcula o tamaño da proxección dun segmento de tamaño 5 sobre a recta da figura, cando é perpendicular a ela e cando é paralela. Depende a proxección da distancia á recta?
10. TEOREMA DA ALTURA
Enunciado 1: Nun triángulo rectángulo, a altura trazada sobre a hipotenusa é media proporcional entre as dúas partes en que divide esta.
No triángulo rectángulo da escena ABC trazouse a altura AD sobre a hipotenusa BC, cumpríndose para calquera triángulo rectángulo a igualdade:


Esta unidad interactiva requiere la máquina virtual de Java J2RE.  

A razón pola que se cumpre esta igualdade é porque a altura AD divide ó triángulo ABC noutros dous que son semellantes e polo tanto seus lados son proporcionais. Son semellantes porque teñen os ángulos iguais (ambos son rectángulos e os dous ángulos agudos teñen seus lados perpendiculares).

10.1-Move o punto de control A e observa como varían os valores dos segmentos AD, BD e DC pero mantéñense iguais entre si, os cocientes BD/AD e AD/DC.

10.2- Modifica o valor da hipotenusa e move o punto A para que apareza o triángulo rectángulo.

10.3- Debuxa no teu caderno un triángulo rectángulo de lados 10, 8 e 6, traza a altura sobre a hipotenusa e comproba que se cumpre o teorema da altura. Contrasta os valores cos da escena Descartes.
Enunciado 2: O cadrado da altura sobre a hipotenusa é igual ó produto das proxeccións dos catetos sobre ela
11. TEOREMA DO CATETO
Enunciado 1: Nun triángulo rectángulo cada cateto é media proporcional entre a hipotenusa e a súa proxección sobre ela.
Como no caso anterior, a altura trazada sobre a hipotenusa divide o triángulo noutros dous semellantes e cúmprense as igualdades seguintes:

Esta unidad interactiva requiere la máquina virtual de Java J2RE.

Move o punto de control A e observa como varían os valores de cada cateto e súas proxeccións sobre a hipotenusa, verificándose en todo momento as igualdades antes indicadas. Modifica o valor da hipotenusa e move o punto A para que apareza o triángulo rectángulo.

11.1- Se a altura sobre a hipotenusa dun triángulo rectángulo divide esta en dous segmentos de medidas 7 e 4, aplica o teorema do cateto para achar os valores de cada un dos catetos.
11.2- Comproba na escena os valores calculados.
11.3- Acha a área do devandito triángulo.
Enunciado 2: Nun triángulo rectángulo o cadrado dun cateto é igual ó produto da hipotenusa e a súa proxección sobre ela.
   
           
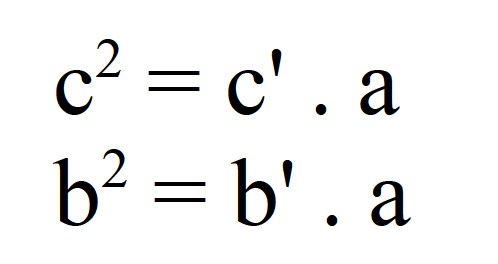  Adaptación: Mª Isabel Hermida Rodríguez
 
© Ministerio de Educación, Política Social y Deporte. Año 2009
 
 

Licencia de Creative Commons
Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.