Se dan una circunferencia con diámetro AB y la recta tangente a ella en el punto B. Por el punto A se traza una semirrecta que corta a la circunferencia en el punto C y a la recta tangente dada en el punto D; en ella se ha marcado un punto M tal que AM = CD. Al girar la semirrecta AC alrededor del punto A, varía la longitud del segmento AM y el punto M describe una curva denominada cisoide de Diocles.

Sorry, the GeoGebra Applet could not be started. Please make sure that Java 1.4.2 (or later) is installed and active in your browser (Click here to install Java now)

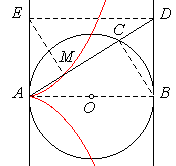
          Como AB es un diámetro de la circunferencia dada ABC es un triángulo rectángulo con ángulo recto en el vértice C. Ahora, si E es el punto simétrico de B con respecto al punto medio de la secante AC y puesto que CD = AM entonces el triángulo DEM es también rectángulo. Esto nos permite realizar otra construcción de la cisoide.

 

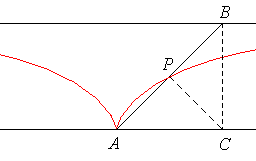
          Sean r y r' dos rectas paralelas y A un punto fijo en la recta r. Dado un punto cualquiera B en la recta r' sean C el pie de la perpendicular a r por C y P el pie de la perpendicular al segmento AB por C. Al variar el punto B sobre la recta r' el punto P describe la curva cisoide de Diocles.