
 |
XEOMETRÍA ANALÍTICA |
| REPASO DE VECTORES | |
| 1. VECTORES . COORDENADAS | |
|
Dous puntos do plano A e B, determinan un vector fixo AB, no que A é a orixe e B é o extremo.
A distancia entre A e B (lonxitude do segmento AB) chámase módulo do vector e a recta que pasa por A e B é a dirección do vector. O sentido é o que vai de A a B. Se as coordenadas do punto A son (a1, a2) e as de B son (b1, b2) as coordenadas do vector AB son (b1-a1, b2-a2). Un vector V está formado por todas as flechas que indican a magnitude, orientación e sentido dese desprazamento. Se tomamos unha desas flechas cuxa orixe coincida coa orixe de coordenadas, ás coordenadas (x,y) do extremo dese vector chamáselles coordenadas do vector. O módulo dun vector calcúlase mediante a raíz cadrada da suma dos cadrados das súas coordenadas, é dicir a raíz cadrada de x2 + y2 . Todas as flechas paralelas a esta co mesmo sentido e tamaño chamáselles equipolentes á primeira. Cando movemos unha figura no plano desprazámola unha certa cantidade nunha dirección e nun sentido |
| 1.-
Representa no teu caderno un vector cuxa orixe sexa (1,0) e o
extremo (-4,1) e calcula as súas coordenadas. 2.- Dado o vector de coordenadas (-3, 5), calcula as coordenadas do extremo, sabendo que as coordenadas da súa orixe son (2, 4). Calcula o módulo. 3.- Sabendo que as coordenadas da orixe do vector (4, -5) son (1, 6), calcula as coordenadas do extremo. 4.- Escribe tres vectores con módulo 9. Poderías escribir máis? |
| Suma de vectores libres | |
| Dados dous vectores U e V defínese a suma como o vector S cuxas coordenadas son a suma das coordenadas de cada un deles. | 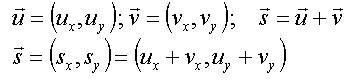 |
|
|||||||
| Regina Puente Fernández | ||
 |
||
| © Ministerio de Educación, Política Social y Deporte. Año 2010 | ||

Os contidos desta unidade didáctica están baixo unha licencia de Creative Commons
se non se indica o contrario.