Moi a miúdo atópase na práctica que existe unha relación entre dous (ou máis) variables. Por exemplo: os pesos dos homes adultos dependen en certo modo das súas alturas; as lonxitudes das circunferencias e as áreas dos círculos dependen do radio, e a presión dunha masa de gas depende da súa temperatura e do seu volume.

Se todos os valores das variables cumpren exactamente unha relación exacta, entón dise que as variables están perfectamente correlacionar ou que hai unha correlación perfecta entre elas ou, máis sinxelamente, que existe unha función ou unha fórmula que as relaciona.

Así a lonxitude L dunha circunferencia e o seu radio r están perfectamente correlacionar pois se verifica exactamente que:

L  = 2p r

Pola contra, se se lanzan simultaneamente dous dados unhas cantas veces, non existirá unha relación entre os puntos que se obteñan en cada dado (salvo que os dados estean cargados), é dicir non existirá correlación entre as puntuacións de cada dado.

Noutros casos, parece que existe certa correlación, aínda que esta non sexa perfecta. Por exemplo, as variables altura e peso dos individuos parecen ter certo grao de relación aínda que non exista unha fórmula que nos permita adiviñar o peso dun individuo coñecida a súa altura.

Entón, xurde a seguinte pregunta fundamental:

¿En qué medida están relacionados a altura e o peso dun individuo?

Se somos capaces de atopar unha forma de medir axeitadamente esa relación, entón, por exemplo, podemos decidir se a altura e o peso dun individuo están mais relacionados entre si que a altura dese individuo e a altura do seu pai.

Cando se busca unha medida para medir esa relación dise que se está a buscar medir a correlación entre esas dúas variables.

Polo tanto, descubrir a correlación entre dúas variables refírese sempre a achar unha medida da relación entre esas dúas variables.

Cando se trata de dúas variables soamente, fálase de correlación simple e cando se trata de máis de dúas variables fálase de correlación múltiple.

Aquí imos tratar soamente da correlación simple.

Volvendo ao exemplo da altura e o peso dun individuo, e aínda que todos aceptemos que non existe unha fórmula exacta que relacione esas dúas variables, si que parece bastante difícil (aínda que non totalmente imposible, en principio) que unha persoa de 120 quilogramos de peso mida 80 centímetros de altura.

É dicir, xorde outra pregunta fundamental:

¿Poderiamos achar unha fórmula para estimar -siquiera aproximadamente- o peso dun individuo a partir da súa altura (ou ao revés)?

Cando se busca unha fórmula dese tipo dise que se está a buscar unha regresión entre esas dúas variables.

Polo tanto, achar unha regresión entre dúas variables refírese sempre a achar unha fórmula ou ecuación que represente a relación aproximada entre esas dúas variables.

E da mesma forma que antes, cando se trata de dúas variables soamente, se fala de regresión simple. Cando se trata de máis de dúas variables fálase de regresión múltiple.

Aquí imos tratar soamente da regresión simple.

ACTIVIDADE 1

NUBE DE PUNTOS

Para estudar e medir a relación entre dúas variables, o primeiro paso é recoller os datos que mostren os correspondentes valores das variables consideradas.

Por exemplo, se dispoñemos dos datos da altura e do peso de 100 individuos, o primeiro sería representar nun gráfico cartesiano os 100 puntos (x,y) onde x e e serían a altura e o peso respectivo de cada individuo.

O conxunto de puntos que así obtense adóitase denominar diagrama de dispersión ou mais sinxelamente nube de puntos.

Por exemplo, na escena seguinte pódese contemplar unha nube de puntos real, obtida a partir de datos reais dos que logo falaremos.

Actividades:

Observarás que a nube de puntos está constituída por doce elementos, denominados coas doce primeiras letras do alfabeto.

Se fas "clic" sobre cada punto verás que aparecen as súas coordenadas.

Se che apetece, podes xogar cos outros botóns e non te preocupes se te equivocas, pois sempre podes volver á situación inicial pulsando o botón denominado inicio.

De feito, necesariamente deberás manexar eses botóns para ver o punto L, que non se atopa na imaxe inicial.

Actividade 1.1. - O que che pedimos, en primeiro lugar, é que escribas nun papel as coordenadas de cada un dos doce puntos.

A primeira coordenada corresponde ao dato estatístico do chamado Índice de Prezos Industriais (IPRI), elaborado polo Instituto Nacional de Estatística (INE) e que é un dato que pretende medir a evolución dos prezos dos produtos industriais.

A segunda coordenada corresponde ao chamado IBEX-35 que é o índice de referencia mais importante da Bolsa española. Para facilitar a súa representación na escena anterior, os valores reais dividíronse por 100.

Na Bolsa de Nova York, a aparición do IPRI americano ten grande influencia, cousa que non acontece (ata agora) na Bolsa española.

Precisamente, o que tratamos de estudar é qué correlación existe entre ambas as dúas variables e se sería posible estimar o IBEX-35 a partir do IPRI.

Os datos que se usaron nos doce puntos corresponden aos doce últimos datos mensuais de ambas as dúas variables, dispoñibles o 1 de xaneiro do ano 2000.

Como dato mensual do IBEX-35 usouse o de peche do primeiro día hábil na Bolsa de cada un dos doce meses de 1999.

Respecto ao IPRI, o dato usado é o máis recente en cada un deses primeiros días hábiles, é dicir o que hipoteticamente pode influír máis. Concretamente, os 12 datos do IPRI usados son os correspondentes a novembro e decembro de 1998 e os dez primeiros meses de 1999.

Actividade 1.2. - En segundo lugar, o que che pedimos é que estudes detidamente a nube de puntos anterior e que intentes seleccionar aqueles puntos que che parecen mais "raros" ou que se afastan mais do resto (anótaos na túa folla de traballo).

ACTIVIDADE 2

RECTA DE AXUSTE

Co diagrama de dispersión ou nube de puntos, é posible frecuentemente representar unha curva que se aproxime aos datos.

Tal curva chámase curva de aproximación.

Na maior parte das nubes de puntos obtidas a partir de casos reais é difícil imaxinarse cál sería a mellor curva de aproximación e, xeralmente, hai que optar por unha determinada (usando algúns criterios específicos) que se adoita denominar curva de axuste.

Nós imos usar como criterio o da simplicidade e dado que a curva mais sinxela é a recta, imos optar por buscar unha recta de axuste que se axuste axeitadamente á nosa nube de puntos.

Dende logo, a forma mais sinxela de obter unha recta de axuste é debuxando unha recta enriba da nube de puntos, tratando de que a devandita recta se axuste o mellor posible á nube de puntos.

Observa a escena seguinte e comproba que podes obter outra recta movendo o punto P e modificando a pendente m. Para mover o punto P podes arrastralo directamente co teu rato, ou ben usar os controis situados debaixo da escena e para modificar a pendente m podes usar o control da pendente situado tamén debaixo da escena e non esquezas que sempre podes volver á posición inicial pulsando o botón inicio.

Actividades:

O que intentamos é atopar graficamente unha boa recta de axuste.

Actividade 2.1. - Lo que che pedimos agora é que escollas aquela recta que, na túa opinión, se axuste mellor á nube de puntos.

Para iso, feixe todas as probas que consideres necesarias e, cando escollas a túa recta de axuste, apunta o valor da pendente e as coordenadas do punto usado, de modo que poidas comparar posteriormente a túa elección coa elección dos matemáticos.

ACTIVIDADE 3

RECTA DE REGRESIÓN POR MíNIMOS CADRADOS

É doadamente comprensible que os matemáticos intentaran atopar un procedemento común para seleccionar a mesma recta de axuste, de modo que todo o mundo estea de acordo e non haxa que aterse a opinións subxectivas.

A recta de axuste seleccionada polos matemáticos é a chamada Recta de regresión por mínimos cadrados e que se obtén seleccionando de entre todas as rectas de axuste posibles, aquela que fai mínimo a suma dos cadrados das distancias verticais dos puntos á recta (agora explicámosche todo isto).

Actividades:

A partir da escena anterior, podes facerte unha idea de como os matemáticos seleccionaron a súa mellor recta de axuste.

O que fixeron é seleccionar aquela recta que fai mínimo o resultado de sumaro cadrado de cada unha das lonxitudes representadas en cor carmesí.

Isto fíxose así por diversas razóns pero é importante precisar que se podía facer doutra forma e que, mesmo, en determinados casos especiais prefírese usar outro criterio para a selección da mellor recta de axuste, aínda que o caso aquí desenvolvido é, dende logo, o máis frecuente.

Ese cadrado (de cada unha dos segmentos de cor carmesí) pódese imaxinar como a área de cada un dos cadrados que poderían construirse sobre cada un deses segmentos de cor carmesí.

Actividade 3.1. - O que che pedimos agora é que escollas aquela outra recta que, na túa opinión, se axuste mellor á nube de puntos, usando o criterio dos matemáticos.

Para iso, fai todas as probas que consideres necesarias e, cando escollas a túa recta de axuste usando o criterio dos matemáticos, apunta o valor da pendente e as coordenadas do punto usado, de modo que poidas comparar posteriormente a túa elección co resultado correcto, calculado matematicamente con toda exactitude.

ACTIVIDADE 4

ECUACIÓN DA RECTA DE REGRESIÓN POR MíNIMOS CADRADOS

A continuación imos indicar cál é a ecuación da recta de regresión por mínimos cadrados, sen entrar nas demostracións matemáticas exactas.

Para calcular a ecuación da recta de regresión por mínimos cadrados faise o seguinte, que explicamos paso a paso, indicando tamén as fórmulas exactas.

• Calcúlase a media aritmética ( ) e a desviación típica ( )dos datos da primeira variable. No noso caso, débese calcular a media aritmética e a desviación típica das coordenadas "x" dos puntos da nube de puntos.

• Calcúlase a media aritmética dos datos da segunda variable ( ). No noso caso, débese calcular a media aritmética das coordenadas e dos puntos da nube de puntos.
• Calcúlase a chamada covarianza entre as as dous variables ( ). No noso caso, débese calcular a covarianza entre as coordenadas "x" e "y" dos puntos da nube de puntos.

As fórmulas exactas para o anterior son as que seguen.

Denotamos aos doce puntos da nube de puntos do seguinte xeito:

(x , y) , (x , y) , ... ,(x ,y )

Entón, tense:

  =

=

=

= + +  . . .  +

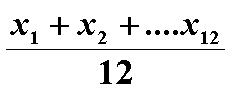
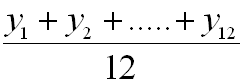
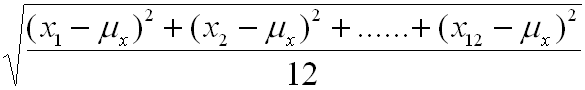
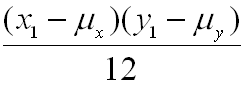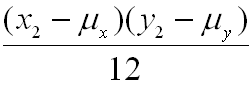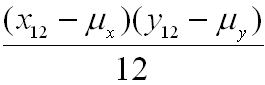
Feito todo o anterior, obténse a ecuación da recta de regresión por mínimos cuadrados da forma seguinte:

y - = m (x - )

onde a pendente m é igual a:

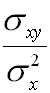
É dicir que a recta de regresión por mínimos cadrados é a recta que pasa polo punto

(,) e que ten por pendente a: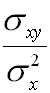

E se aplicamos as fórmulas anteriores á nosa nube de puntos (e redondeando para usar só tres decimais), resulta a recta seguinte, que é á recta de regresión por mínimos cadrados da nosa nube de puntos:

y = 15,283 + 0,711x

Na seguinte escena, representamos en cor carmesí á devandita recta de regresión por mínimos cadrados da nosa nube de puntos e trátase de que a compares coas túas rectas de axuste obtidas anteriormente, nas actividades 3.1 e3.2 anteriores.

Actividades:

Usando os controis inferiores da escena, representa nela ás túas rectas de axuste (seleccionadas nas actividades 3.1 e 3.2 anteriores) e compáraas coa recta matematicamente obtida e que figura representada en cor carmesí.

Actividade 4.1. -O que che pedimos agora é que escribas un breve informe, tratando de explicar os teus resultados en comparación á recta de regresión por mínimos cadrados e, especialmente, tratando de indicar se a recta de axuste dos matemáticos che parece unha boa opción, é dicir se se axusta ben á nube de puntos (na túa opinión) ou non e as razóns de todo iso.

ACTIVIDADE 5

COEFICIENTE DE CORRELACIÓN LINEAL

A continuación imos falar da medida usual de correlación lineal entre dúas variables, o chamado Coeficiente de correlación lineal ( , léase "ro").

Feito todo o anterior, é moi doado calcular o devandito coeficiente, a partir da fórmula seguinte:

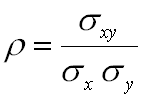
onde se define de forma análoga a , é dicir:

=

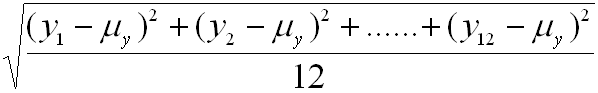
O que este coeficiente mide é o grao de axuste da recta de regresión a unha determinada nube de puntos.

Canto maior sexa este axuste, máis confiados debemos estar en que é correcto usar a unha recta como modelo da nosa nube de puntos, pero se o axuste non se considera bo, deberemos pensar que a nosa nube de puntos non se representa ben por unha recta e haberá que buscar outros modelos (quizais a nosa nube de puntos se axuste mellor a unha parábola, por exemplo).

Convén tamén destacar que a partir da definición anterior, se pode comprobar que a ecuación da recta de regresión pode expresarse tamén como:

y - = m(x - )

onde a pendiente m é igual a:

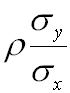
É dicir que a recta de regresión por mínimos cadrados é a recta que pasa

(,) e que ten por pendente   :

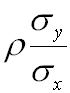
Algunhas consideracións importantes sobre o coeficiente de correlación lineal:

• É unha cantidade sen dimensións, é dicir non depende das unidades empregadas. Por exemplo, se se está a buscar achar o coeficiente de correlación entre o peso e a altura dos nenos en determinada cidade, entón o resultado será o mesmo independentemente de se o peso de todos os nenos se mide en Quilogramos ou en gramos e independentemente de se a altura de todos os nenos se mide en metros ou centímetros.

• Verifícase sempre que:

    -1 1

• Se o coeficiente de correlación é igual a 1, entón hai unha correlación lineal positiva perfecta, é dicir que os datos se axustan perfectamente a unha recta de pendente positiva, é dicir unha recta que crece, ou sexa que cando x aumenta, entón tamén o fai e.

• Se o coeficiente de correlación é igual a -1, entón hai unha correlación lineal negativa perfecta, é dicir que os datos se axustan perfectamente a unha recta de pendente negativa, é dicir unha recta que decrece, ou sexa que cando x aumenta, entón e diminúe.

• En calquera outro caso, para aceptar se hai unha correlación lineal aceptable, non hai ningunha regra estrita. Normalmente, para aceptar a existencia da devandita correlación, o coeficiente debe ser maior que 0,7 ou menor que -0,7. No caso contrario, adóitase rexeitar a existencia de correlación lineal.

¿Que pode deducirse se se rexeita a existencia de correlación lineal se, por exemplo, se atopa un coeficiente de correlación lineal de 0,3 entre dúas variables?

• O único que pode deducirse é que os datos non se axustan a unha recta.

• Pero isto non significa que non haxa relación entre eles dado que poderían axustarse a unha parábola ou a calquera outra curva. Só se deduce que non hai correlación lineal aínda que puidese haber unha correlación non lineal.

• Este é o grande inconvinte do coeficiente de correlación lineal: non serve para decidir se hai ou non unha posible relación entre dúas variables, só serve para decidir se hai ou non unha posible relación lineal entre dúas variables.

• Iso fai que, definitivamente, o único xeito de decidir inicialmente se debe sospeitarse ou non a existencia de relación entre dúas variables é estudar detidamente o diagrama de dispersión correspondente, ou sexa a nube de puntos.

• E, no seu caso, sóo despois habrá que decidir con que curva se intentan axustar os datos.

Actividades:

Usando a fórmula anterior e os datos obtidos na actividade 1.1 imos facer un exercicio de cálculo do coeficiente de correlación lineal e outros dous de estudio de predicións (a partir dos doce datos da nube de puntos, obtida con datos do IPRI e do IBEX-35).

Actividade 5.1. - O que che pedimos agora é que calcules o coeficiente de correlación lineal entre o IPRI e o IBEX-35, a partir dos datos da nube de puntos e, en función do resultado que obteñas, indiques se, na túa opinión, se pode dicir ou non que os devanditos IPRI e IBEX-35, están ou non correlacionar linealmente.

Actividade 5.2. - E agora trátase de comparar os resultados do IBEX-35 cos que se obteñen a partir da recta de regresión. Para iso, o único que tes que facer é (na ecuación que xa calculamos da recta de regresión, é dicir: y =15,283 + 0,711x) substituír a x por cada un dos valores do IPRI e comparar o resultado que se obtén co correspondente valor real do IBEX-35 e aconsellar sobre se vale a pena ou non xogar o diñeiro na bolsa usando o IPRI como mecanismo de predición.

Actividade 5.3. - A partir dos datos do IPRI (que son públicos e que se poden obter no INE ou ni IGE( http://www.ine.es http://www.ige.es, por exemplo), realiza as túas propias predicións do IBEX-35 baseándose nos datos do IPRI e compara logo os resultados obtidos usando os datos do IBEX-35 publicados en calquera xornal.

Autora: Monica Escudero Baylin traducida por Adelino Pose Reino
 

	© Ministerio de Educación y Ciencia. Año 20080