
Bolígrafo digital
Enlaces
Título:
Continuidad. Representación gráfica de funciones.
Nivel:
1º Bachillerato (ambas modalidades)
Profesor:
Joan Carles Fiol Colomar
Descripción:
Representación y estudio de la continuidad de funciones elementales y definidas a trozos. Transformaciones de funciones. Corrección de un examen.
Preparación previa:
Diseño de plantillas (cuadrícula con ejes de coordenadas con y sin funciones representadas, modelo de un examen, ...) importadas desde archivos pdf.
Desarrollo:
En diferentes sesiones (2-3 horas en cada grupo de primero de bachillerato, uno de cada modalidad) se han realizado las siguientes actividades:
1. Corrección de una prueba de evaluación.
Una vez realizada una prueba de evaluación, esta se corrigió de forma manuscrita usando el bolígrafo sobre un plantilla en pdf de la propia prueba, mientras el alumnado tenía la suya en frente para observar y corregir sus errores:
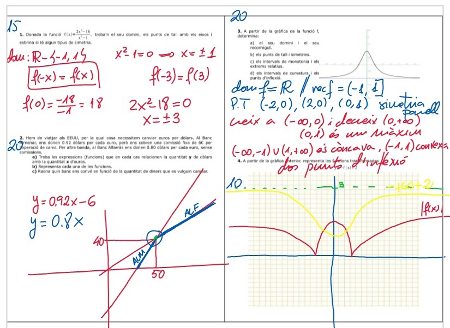
2. Transformaciones de una función polinómica.
En el archivo preparado sobre hoja interactiva, la gráfica de una función polinómica y=f ?x ? el ejercicio consiste en representar sobre la misma cuadrícula, diferentes funciones transformadas, del tipo:
y=f (x + a), y=f (x) + b, y= |f(x)|, y=−f(x)
Para ello, resulta ideal el uso de diferentes colores. Aquí uno de los ejercicios realizado con y por los alumnos.
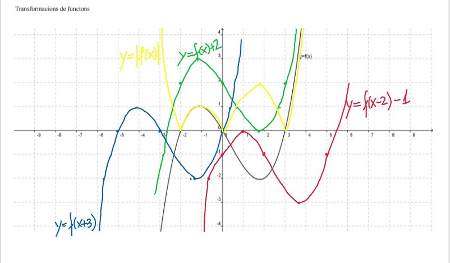
3. Representación gráfica de una función definida a trozos.
Sobre una hoja interactiva con una cuadrícula y ejes de coordenadas, se representan diferentes funciones definidas a trozos, a partir de funciones elementales. Al mismo tiempo, se estudia la continuidad de forma gráfica. Otra situación en la que los colores resultan muy interesantes para diferenciar los “trozos” y también usar diferentes grosores a la hora de resaltar los distintos elementos de la función (asíntotas, puntos de corte, ...). Una imagen de muestra:
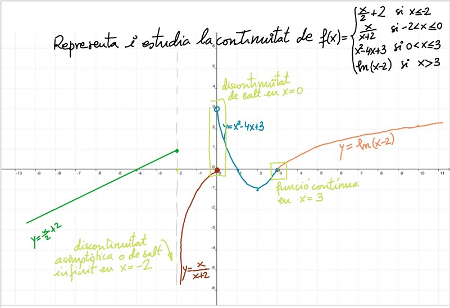
4. Estudio de la continuidad de funciones definidas a trozos.
En este caso, se estudia la continuidad de dos funciones sin la gráfica, aplicando directamente la definición de función continua. Aunque no fuese imprescindible, se utilizaron diferentes colores para distinguir el estudio en los diferentes puntos a considerar. Otra imagen:

Valoración del profesor:
Mi intención inicial era usar el bolígrafo con 3o de ESO y con 1o de bachillerato, pero un cambio imprevisto en una salida de una semana de los de 3o, hizo que sólo pudiera hacerlo con los de bachillerato.
Al usarlo el primer día con la corrección de la prueba de evaluación, me fui situando en diferentes lugares del aula para comprobar la cobertura y alcance (es un aula de unos 60 m2), lo que provocó cierto desconcierto inicial en los alumnos, ya que al mismo tiempo querían mirar la pantalla y también me buscaban con la mirada. Al poco tiempo, se adaptaron. Respecto a la recepción del bolígrafo, es satisfactoria, solamente destacar ligeros parpadeos en algún trazo, dependiendo de la distancia y de la velocidad en la escritura.
Las prácticas siguientes fueron compartidas con el alumnado. Tenían una serie de ejercicios para resolver en casa. En clase se corrigieron dichos ejercicios utilizando el bolígrafo por parte de los alumnos y alumnas. No tuvieron ningún problema en su utilización. Había que controlar dos cosas (ya que todo el material se exportaría a pdf y estaría accesible en el servidor del centro para que les sirviera de apuntes): primero, había que escribir con “buena letra”, para que todos lo entendieran bien, y, en segundo lugar, había que procurar que las “líneas” de las gráficas fueran más o menos uniformes (aquí me incluyo yo mismo). Tampoco fue problema para ellos y ellas, enseguida aprendieron eliminar escritura y trazos, intentando escribir de nuevo con mejor letra y trazo más nítido y uniforme. Es importante destacar que, al no haber nadie en la pizarra, hizo que todos estuvieran más pendientes de lo que se estaba escribiendo y por tanto más participativos, la corrección de los ejercicios era más colaborativa.
Aunque no la he utilizado con los alumnos, el hecho de que el bolígrafo incorpore una calculadora, con la posibilidad de medir distancias y ángulos sobre un gráfico o sobre una imagen, abre un montón de posibilidades para trabajar en semejanza, trigonometría, geometría, ...
Para mí ha sido una experiencia muy satisfactoria, aunque también “extraña” (llevo más de veinte años explicando desde la pizarra). Creo que puede ser una herramienta muy útil, complementaria a las PDI, que además puede resolver la timidez y nerviosismo de algunos (o muchos) alumnos al salir a la pizarra.
Como sugerencias de mejora, primero, yo pediría que los archivos en pdf también se pudieran importar en formato vertical (por tanto, que hubiera hojas con los dos formatos: vertical y horizontal), ya que es el formato que deben utilizar normalmente mis alumnos en la entrega de sus trabajos, de esta manera podría corregirlos y anotar comentarios manuscritos sin imprimirlos (incorporar dos páginas en una, reduce demasiado el tamaño) y, en segundo lugar, habría que “reducir” el consumo de batería (de momento, confiaremos en las pilas recargables).
Valoración de los alumnos:
La valoración más comentada por unanimidad ha sido el hecho de poder escribir en la “pizarra” sin tener que salir a la pizarra. Además, al estar sentados normalmente por parejas, el compañero o compañera siempre puede dar una ayudita. También han comentado que no hay que esperar a que el profesor (o alumno) termine de escribir y se aparte para poder ver todo lo que se ha escrito.
Otro aspecto muy valorado por la mayoría ha sido la posibilidad de trabajar con diferentes colores y con diferentes trazos, lo cual permite diferenciar y resaltar partes de los textos y de los gráficos según convenga.
A un alumno (¡no demasiado trabajador!) le ha gustado mucho el hecho de que todo lo que se escribe con el bolígrafo puede guardarse y exportarse a pdf (“Así no tendré que tomar apuntes ni hacer fotocopias”!!!)
En general, a todos los alumnos les gustó mucho la experiencia y me sugirieron que lo utilizara en todas las clases.
 Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-CompartirIgual 3.0 España
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-CompartirIgual 3.0 España