


| Mª Josefa Grima Javier Soriano |
|
Imprimir |
|
ECUACIÓN DE LAS ONDAS ESFÉRICAS |
||
|
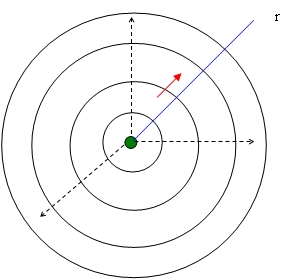
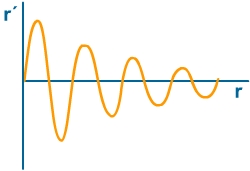
Como consecuencia de esta disminución de intensidad con la distancia al foco ( que llamamos ATENUACIÓN DEL M.O.) la amplitud en la vibración de las partículas del medio debe depender de “r” ya que la frecuencia “f” es constante. Por tanto dicha amplitud en la vibración de las partículas en una onda esférica será :
| ||
 |
 |
|
| Ondas sonoras armónicas | ||
| Ondas sonoras armónicas | ||
| Ecuación de las ondas sonoras | ||
| Frecuencia y longitud de onda | ||
| Tono | ||
| Ondas de presión |
| Estudio energético de las ondas sonoras | ||
| Intensidad de una onda | ||
| Factores de los que dependen la intensidad | ||
| Ondas planas y ondas esféricas | ||
| Ecuación de las ondas esféricas | ||
| Escala en decibelios |
| Ondas estacionarias | ||
| Introducción | ||
| Ecuación de las ondas estacionarias armónicas | ||
| Los tubos sonoros | ||
| Los armónicos |