Experimentación en el aula
Funciones: Polinómicas y Racionales
- El Grupo
El grupo con el que he realizado la experiencia es 4º de ESO y la asignatura Matemáticas Opción A. El grupo está formado por 10 alumnos, 3 chicas y 7 chicos.
- Objetivos y Contenidos:
Los objetivos y contenidos que he tratado han sido los previstos en las unidades 12 y 13 de la programación del Departamento de Matemáticas de mi Centro.
- Unidad: Funciones.
- OBJETIVOS:
• Comprender el concepto de función de variable real, expresarla en distintos modos (tablas, gráficas, etc.) y reconocer las principales características de las mismas.
• Comprender y representar funciones definidas a trozos.
• Reconocer la tasa de variación media como medida de la variación de una función en un intervalo, y aplicarla para determinar la continuidad y el crecimiento o decrecimiento de una función.
• Analizar gráficas de funciones de variable real.
- CRITERIOS DE EVALUACIÓN:
• Distinguir una función de variable real, la variable dependiente y la variable independiente; obtener una gráfica a partir de su tabla y viceversa, y reconocer sus principales características: dominio, recorrido, simetría, periodicidad, máximos y mínimos relativos y absolutos, signos y puntos de corte.
• Calcular la imagen de un punto del dominio de una función definida a trozos y representarla gráficamente.
• Definir y calcular la tasa de variación y la tasa de variación media de una función de variable real en un intervalo.
• Calcular los conceptos de tasa de variación y de tasa de variación media, y aplicarlos para determinar la continuidad y el crecimiento o decrecimiento de funciones de variable real sencillas.
• Establecer las características básicas de una función a la vista de su gráfica, e interpretar gráficas o tablas que representen situaciones sobre la vida cotidiana.
- CONTENIDOS:
- Conceptos
• Función de variable real. Variable independiente y variable dependiente.
• Formas de expresar una función:expresión algebraica, tabla de valores y gráfica.
• Dominio y recorrido de una función.
• Función definida a trozos.
• Puntos de corte de una función con los ejes de coordenadas y signos.
• Simetría de una función. Función par y función impar.
• Periodicidad de una función. Periodo de una función.
• Tasa de variación de una función en un intervalo.
• Tasa de variación media de una función en un intervalo.
• Continuidad y discontinuidad de una función.
• Intervalos de crecimiento y decrecimiento de una función.
•Máximos y mínimos relativos y absolutos de una función.
- Procedimientos
• Reconocer una función de variable real, y distinguir la variable independiente y la variable dependiente.
• Interpretar y elaborar tablas de valores a partir de datos numéricos, gráficas, fórmulas, etc., y obtener la gráfica de una función utilizando una tabla de valores.
• Obtener el dominio, el recorrido, los puntos de corte con los ejes y los signos de una función a partir de su gráfica o de su expresión algebraica.
• Representar funciones definidas a trozos a partir de su expresión algebraica y viceversa.
• Reconocer si una función es simétrica o periódica, indicando el tipo de simetría o periodo que presentan.
• Calcular la tasa de variación y la tasa de variación media de una función en un intervalo cerrado, e interpretar su significado.
• Utilizar la tasa de variación para determinar los intervalos de crecimiento y decrecimiento.
• Comprobar la continuidad de una función en un punto.
• Determinar los máximos y los mínimos relativos y absolutos de una función a partir de su gráfica.
• Reconocer las características de una función sencilla a partir de su gráfica o de su expresión algebraica, utilizando el vocabulario y la nomenclatura adecuados.
- Actitudes
• Apreciación de la precisión y utilidad de los lenguajes gráficos para representar y resolver problemas de la vida cotidiana.
• Gusto por la resolución de situaciones científicas, usando la representación de funciones como un método preciso y práctico.
• Sentido crítico ante los resultados obtenidos al representar una función.
• Curiosidad y tenacidad en la búsqueda de relaciones entre magnitudes o fenómenos.
• Valoración crítica frente a informaciones de carácter funcional que aparecen en los medios de comunicación.
• Satisfacción y gusto por la presentación cuidadosa y ordenada de los trabajos.
- Unidad: Funciones racionales y polinómicas.
- OBJETIVOS:
• Definir, representar y obtener la expresión algebraica de funciones polinómicas, potenciales, de proporcionalidad inversa y racionales.
• Aplicar los conocimientos sobre las funciones polinómicas y racionales para representar y comprender mejor fenómenos sobre situaciones cotidianas que pueden ser descritas mediante este tipo de funciones.
- CRITERIOS DE EVALUACIÓN:
• Identificar las parábolas como la representación gráfica de funciones cuadráticas y representarlas gráficamente.
• Reconocer gráfica y analíticamente las funciones potenciales, y representarlas gráficamente
• Distinguir las hipérbolas como la representación gráfica de funciones de proporcionalidad inversa y representarlas gráficamente.
• Reconocer y representar gráficamente las funciones racionales.
• Plantear y resolver problemas utilizando las funciones polinómicas y racionales.
- CONTENIDOS:
- Conceptos
• Funciones cuadráticas.
• Funciones potenciales.
• Funciones de proporcionalidad inversa.
• Funciones racionales.
- Procedimientos
• Identificar una función cuadrática como una parábola.
• Determinar analíticamente el vértice, el eje y los puntos de corte de una parábola con los ejes de coordenadas.
• Identificar el vértice de la parábola con un máximo o con un mínimo de la función cuadrática.
• Representar gráficamente una parábola según sus elementos característicos.
• Representar funciones potenciales y estudiar sus características en función de la paridad del exponente.
• Representar funciones de proporcionalidad inversa, relacionarla con la hipérbola y obtener sus elementos característicos tanto a partir de su gráfica como de su expresión algebraica.
• Dibujar funciones racionales como traslaciones de funciones de proporcionalidad inversa y estudiar sus características.
•Identificar situaciones de la vida cotidiana que se pueden resolver utilizando para su descripción funciones racionales o polinómicas.
- Actitudes
• Valoración de las funciones cuadráticas, potenciales, de proporcionalidad inversa y racional para transmitir informaciones y resolver problemas de la vida cotidiana.
• Satisfacción y gusto por la presentación cuidadosa y ordenada de tablas y gráficas.
• Perseverancia y flexibilidad en la búsqueda de soluciones.
• Gusto por la resolución de situaciones científicas, usando la representación de funciones como un método preciso y práctico.
• Sentido crítico ante los resultados obtenidos al representar una función.
• Curiosidad y tenacidad en la búsqueda del tipo de funcionalidad existente entre magnitudes o fenómenos.
• Valoración crítica frente a informaciones de carácter funcional que aparecen en los medios de comunicación.
- Materiales
Además de la pizarra y la tiza para hacer las introducciones teóricas he utilizado las Unidades Didácticas de Descartes:
Estudio gráfico de características globales de una función de Antonio Caro Merchante (en el índice "Estudio gráfico de características globales de una función").
Funciones elementales de Antinio Caro Merchate (en el índice "Representación e interpretación de gráficas").
- Lugares y condiciones
El lugar usado para la experiencia ha sido el Aula de Informática del centro.
El Aula de Informática dispone de 15 ordenadores, por lo que han podido disponer de uno para cada alumno.
- Temporalización
Hemos dedicado 8 clases de una hora incluyendo la dedicada al "examen".
DESARROLLO DE LA EXPERIMENTACIÓN
Voy a comentar lo más interesante de cada día, recogido en mi cuaderno del profesor.
Sesión 1:
La experiencia se inició el 17 de Mayo. Empiezo definiendo función y el dominio y recorrido de una función. Entramos en la página principal del proyecto Descartes y accedemos a la aplicación "Estudio gráfico de características globales de una función" del índice de aplicaciones. Les dejo que trabajen con las escenas correspondientes a los dos primeros puntos de la unidad: funciones y dominio e imagen. Algunos alumnos preguntan si hay que examinarse de lo que están haciendo.
Sesión 2:
El día 18 les explico cómo hallar el signo y puntos de corte con los ejes de una función, así como la simetría y periodicidad. El resto de la clase lo dedican a trabajar con las escenas correspondientes a "Periodicidad" y "Simetrías" de la aplicación del día anterior.
Sesión 3:
El día 19, estudiamos la tasa de variación, tasa de variación media y la continuidad de una función. Realizan algunos ejercicios del libro de texto, sobre todo de tasa de variación y trabajan las escenas correspondientes a "Continuidad" de la aplicación "Estudio gráfico de características globales de una función".
Sesión 4:
El día 20 explico los apartados del libro "Crecimiento y decrecimiento" y "Maximos y mínimos" y trabajan las escenas correspondientes a "Variación" de la aplicación que hemos estado utilizando.
Sesión 5:
El día 24 empezamos con la Unidad Didáctica "Representación e interpretación de gráficas", hacemos algunos de los ejercicios correspondientes a las escenas de funciones lineales y funciones cuadráticas. Les propongo ejercicios del libro de texto.
Sesión 6:
El día 25 corregimos los ejercicios propuestos y pasamos a "Funciones radicales" y "Funciones de proporcionalidad inversa" de la Unidad Didáctica del día anterior. Les mando algunos ejercicios para casa.
Sesión 7:
El día 26 corregimos los ejercicios propuestos y terminamos la unidad con las funciones potenciales y funciones racionales del libro de texto. Hicimos algunos ejemplos y ejercicios.
Sesión 8:
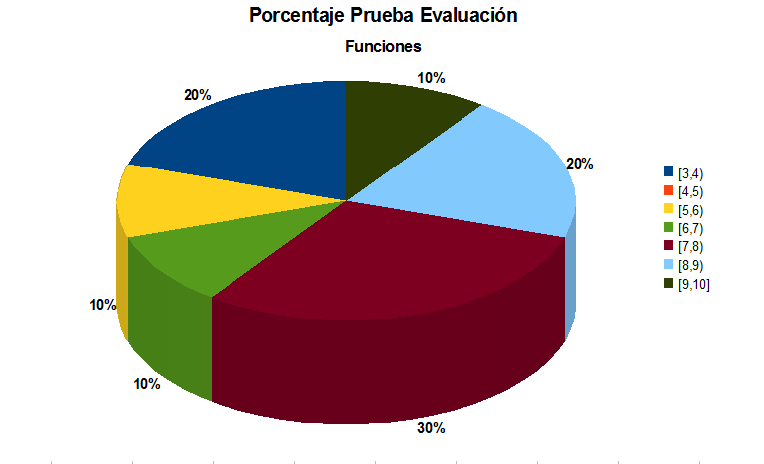
El día 27 hicieron el examen escrito. Cuando terminaron rellenaron la encuesta.
Los resultado obtendos en la prueba de evaluación han sido muy positivos. Puede verse el resumen de los mismos en el siguiente gráfico:
- Encuesta cerrada
| Análisis de la encuesta |
Resultados (medias) |
|
|---|---|---|
| 1º | ¿Te gustan las matemáticas? | 3.2 |
| 2º | ¿Qué nota sueles sacar en matemáticas? | 3.1 |
| 3º | ¿Te interesó la experiencia cuando te la contarón? | 3.4 |
| 4º | Has tenido dificultades para hacer las actividades? | 3.1 |
| 5º | ¿Prefieres este sistema al tradicional? | 3.6 |
| 6º | ¿Cuánto te parece que has aprendido? | 3.4 |
| 7º | ¿Te ha gustado la experiencia? | 3.5 |
| 8º | ¿Te ha gustado trabajar en equipo? | 1 |
| 9º | ¿Te gustaría continuar trabajando con este método? | 3.8 |
| 10º | ¿Crees que es posible aprender matemáticas así? | 4 |
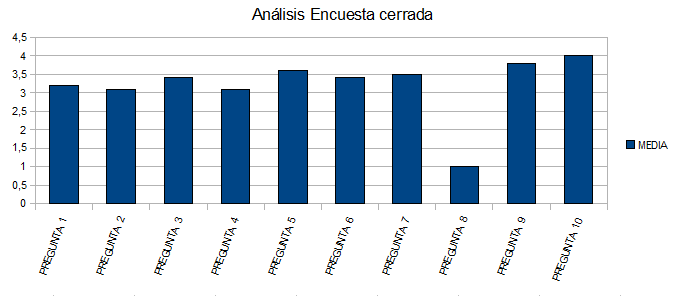
Indicar que el trabajo se ha realizado de forma individual, puesto que cada alumno disponía de un ordenador. Por ello, la media de la pregunta nº 8 es 1.
- Encuesta abierta
1.- Indica qué es lo que más te ha gustado de esta experiencia:
A la mayoría les ha gustado aunque como era de esperar hay algunos a los que les cuesta los cambios.
2.- Indica qué es lo que menos te ha gustado de esta experiencia:
Casi todos coinciden en que les hubiera gustado hacer más ejercicios. Y aunque están acostumbrados a usar el ordenador y les gusta, se sienten más solos.>
3.- Indica lo qué cambiarías y lo que no cambiarías:
Aquí sólo tres alumnos contestan que prefieren el método tradiciona, los demás afirman que no cambiarían nada, que les ha gustado la experiencia.
4.- Si quieres aclarar algunas de las respuestas dadas en la tabla anterior escríbelo aquí:
Nadie contesta.
5.- Expresa tu valoración general o los comentarios que creas que son de interés:
Pocos contestan. Casi todos hacen una valoración positiva de la experiencia.
Mi valoración de esta experiencia ha sido positiva por diversos
motivos: la gran motivación de los alumnos, el alto grado de participación de
los alumnos, los buenos resultados obtenidos y la satisfacción personal.
Por mi parte la experiencia ha sido bastante enriquecedora aunque me ha supuesto un esfuerzo extra, ya que preparar una unidad utilizando las nuevas tecnologías lleva su tiempo, pero espero poder utilizarlo en próximos cursos.
Autor: Mª Carmen Torres Alonso.



