Sistemas de ecuaciones
Experimentación en el aula
La presente unidad didáctica se ha elaborado para un nivel aproximado de 3º de la ESO, siempre cómo complemento de un sistema de enseñanza tradicional. Con esto no quiero decir que no se puedan realizar (o modificar éstas) actividades para realizarlas mediante internet, sino que las he diseñado como complemento.
Situación inicial
Desafortunadamente no he podido realizar la actividad con alumnos de 3º de ESO, ya que el tema lo habíamos terminado hace algún tiempo y, además, andamos con el tiempo justo para cumplir nuestros objetivos. Por el contrario, si que he tenido un grupo de alumnos de 2º de ESO con los que hemos podido llevar a cavo la experiencia.
Se trata de un grupo pequeño de 16 alumnos con una asignatura optativa (de matemáticas), pero tan solo 2 horas semanales. Además, ya habían manipulado los ordenadores con anterioridad al utilizar Geogebra para la representación de objetos en el plano (en concreto hemos realizado una actividad sobre los centros de los triángulos). Esto unido al interés de los estudiantes de no tener una pizarra ante las narices ha facilatado el transcurso de la experiencia.
Desarrollo de la actividad
He dispuesto a los alumnos en parejas, ya que el aula no tenía suficientes ordenadores para todos, pero sobre todo para su colaboración. A la dificultad de manipular un ordenador para usos no lúdicos (como es el uso del nippe Descartes) hay que añadir que, como ya he dicho, la actividad la había diseñado para alumnos de 3º de ESO.
Hemos usado dos sesiones para recordar los conceptos vistos en 1º y tener las bases mínimas para la realización de la actividad sin profundizar demasiado en los métodos algebraicos de resolución, ya que los van a estudiar en breve en 2º y no debemos profundizar en el curriculo de la asignatura de matemáticas en esta optativa.
Las tres sesiones siguientes se han desarrollado con la menor cantidad de explicaciones por mi parte, sobre todo en lo que respecta al uso de las escenas que he construido: tienen las instrucciones para realizarlas en la propia página. Las cuestiones que he respondido han sido más teóricas sobre las ecuaciones y, al mismo tiempo, he intentado suscitar la curiosidad por las respuestas que obtenían y otras nuevas preguntas que les surgían al respecto.
La última sesión la hemos utilizado para contrastar y valorar tanto de lo aprendido como de la propia herramienta en sí, y realizar la encuesta.
Valoración
Les he pasado a los alumnos la encuesta facilitada en el curso, que por si acaso la reproduzco aquí:
| Preguntas | Resultados (medias) |
| 1.- ¿Te gustan las matemática? | 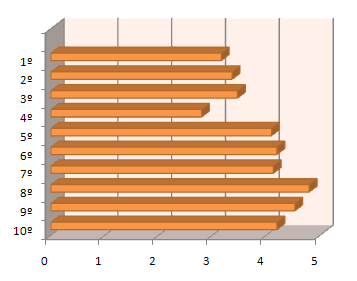 |
| 2- ¿Qué nota sueles sacar en matemáticas? | |
| 3.-¿Te interesó la experiencia cuando te la contarón? | |
| 4.-Has tenido dificultades para hacer las actividades? | |
| 5.-¿Prefieres este sistema al tradicional? | |
| 6.-¿Cuánto te parece que has aprendido? | |
| 7.-¿Te ha gustado la experiencia? | |
| 8.-¿Te ha gustado trabajar en equipo? | |
| 9.-¿Te gustaría continuar trabajando con este método? | |
| 10.-¿Crees que es posile aprender matemáticas así? |
Como puede observarse no se trata de malos alumnos, por lo menos en matemáticas, y por si eso fuera poco les gustan¿?!!!
La peor de las respuestas ha sido a la cuarta pregunta, porque han tenido dificultades al realizar la actividad. Sobre todo lo achaco al tema y al nivel de conocimientos de los alumnos.
El resto de respuestas simplemente me animan y nos deberían animar a todos a realizar actividades de este tipo, o por lo menos a intertarlo. Los alumnos han aprendido y se lo han pasado bien, o eso dicen...
He de añadir que las desviaciones de los resultados son pequeñas, en la mayor de ellas llega a 1, por lo que tienen una opinión bastante uniforme sobre la actividad.
Valoración personal
En general estoy contento con el resultado, aunque creo debería completar y/o modificar los contenidos teóricos y algunas explicaciones para que les resultase más fácil realizarlas. Los alumnos han respondido positivamente ante esta nueva situación a pesar de las dificultades y han mejorado los conocimientos sobre las materia.
Sin embargo, si el objetivo es la enseñanza a distancia, debería completar las nociones teóricas necesariamente y, tal vez, realizar más actividades.




