Introducción a las Funciones.

 Estudio gráfico

INTRODUCCIÓN

    El lenguaje de las gráficas es universal. Basta abrir un periódico, o ver las noticias para comprender que se nos hace necesario saber interpretarlas.

    A través de esta UD aprenderemos a ello, con ayuda del ordenador el cual nos permitirá asimilar las ideas y conceptos de forma más efectiva a la vez que rápida.

    Como complemento, tenéis las mismas actividades en vuestros cuadernos, y los completaréis durante la marcha de esta Unidad virtual.

OBJETIVOS

• Aprender a describir cualitativamente las propiedades de las funciones a partir de la gráfica de la función.
• Adquirir una idea intuitiva de las propiedades de las funciones.
• Familiarizarse con las U.D. virtuales que nos ofrece la web Descartes.
• Valorar la posibilidad de desarrollar próximas U.D. a través del ordenador en el aula de informática.

1.- FUNCIÓN

1º BACHILLERATO C

1. CONCEPTO DE FUNCIÓN (1ª escena)

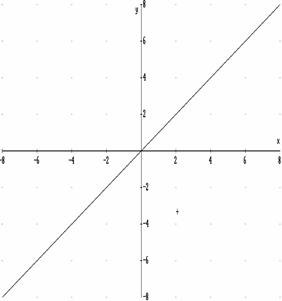
Una función es una relación entre dos variables numéricas, habitualmente las denominamos x e y, a una de ellas la llamamos variable dependiente pues depende de los valores de la otra para su valor, suele ser la y, a la otra por tanto se la denomina variable independiente y suele ser la x.

Pero además para que una relación sea función a cada valor de la variable independiente le corresponde uno o ningún valor de la variable dependiente, no le puede corresponder dos o más valores.

1.-Representa dos gráficas en el siguiente eje de coordenadas, de forma que una corresponda a una función, mientras que la otra no.                                              

2.- DOMINIO E IMAGEN

1º BACHILLERATO C

1. DOMINIO E IMAGEN DE UNA FUNCIÓN

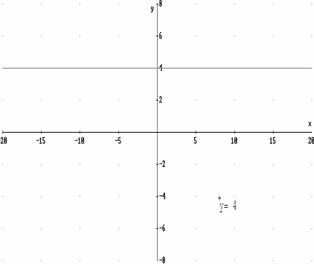
Se llama dominio de definición de una función al conjunto de valores de la variable independiente, x, para los que existe la función, es decir para los que hay un valor de la variable dependiente, y.

Se llama imagen o recorrido de una función a todos los valores de la variable dependiente que tienen algún valor de la variable independiente que se transforma en él por la función.

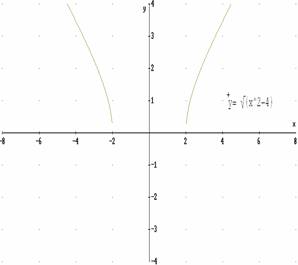
1.- Halla el dominio y el recorrido de las siguientes funciones:

3.- Halla el dominio de las siguientes funciones.

      a) y =        b)y =       c) y =      d)  y =

3.- VARIACIÓN

1º BACHILLERATO C

1. VARIACIONES DE UNA FUNCIÓN

Si observamos una gráfica vemos que en unos puntos la gráfica sube (Crecimiento), otros en los que baja (Decrecimiento) y otros en los que ni sube ni baja, es decir, permanece constante. Estos aumentos o disminuciones de la variable dependiente es lo que denominamos variación de la función. Con las escenas 5, 6 y 7 hemos querido representar cada caso.

1.- Dibuja una función que pase de creciente a decreciente en x=-2 y a su vez pase de decreciente a creciente en x= 1. A partir de x= 2 debe ser constante hasta x= 5.Justo desde ese valor la función crece pronunciadamente hasta más infinito.

2.- Observa la escena siguiente y escribe en tu cuaderno que variación crees que tiene la función representada y entre que valores.

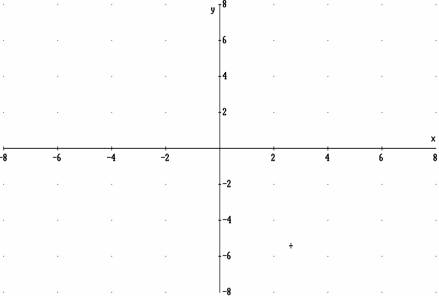
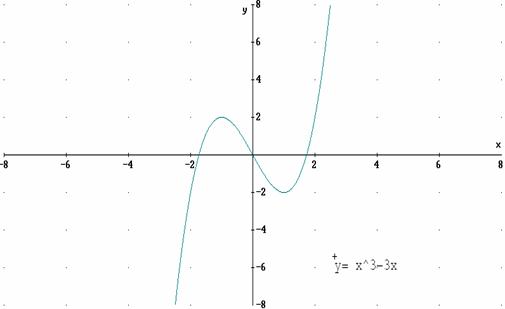
3.-Apunta en tu cuaderno los puntos máximos y mínimos de la función que se representa a continuación:

4.- CONTINUIDAD

1º BACHILLERATO C

1. CONTINUIDAD Y DISCONTINUIDAD DE UNA FUNCIÓN

La idea de función continua es aquella que se puede representar con un solo trazo es decir que no hay que levantar el lápiz para recorrerla en toda su extensión.

En los casos en los que no se pueda representar así será discontinua.

Las discontinuidades podrán ser de varios tipos, observa las escenas siguientes y veras los distintos tipos de discontinuidades.

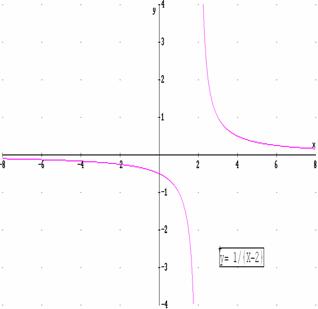
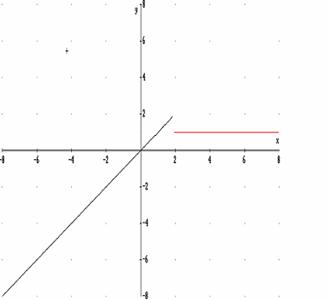
1.- Dibuja en tu cuaderno varias funciones continuas.

2.- Observa en la siguiente gráfica lo que ocurre en el punto x=2; como verás la función no tiene valor, el segmento que une el punto (2,0) con el valor de la función desaparece. ¿Qué pasa en este punto? los valores a la izquierda y a la derecha ¿Cómo son?.

Observa la escena siguiente e intenta contestar a las mismas cuestiones de la escena anterior.

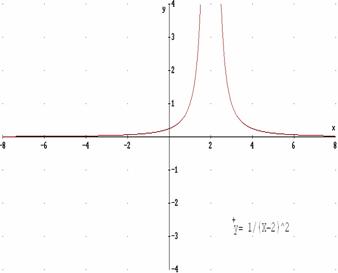
3.- ¿Existe el valor de la función en el punto de abcisa x = 2?

¿Qué pasa en este punto? ¿Cómo son los valores a la izquierda y a la derecha?

Observa las escenas siguientes e intenta contestar en cada caso a las mismas cuestiones de la escena anterior.

4.- ¿Existe el valor de la función en el punto de abcisa x = 2?

¿Qué pasa en este punto? ¿Cómo son los valores a la izquierda y a la derecha?.

5.- PERIODICIDAD

1º BACHILLERATO C

1. PERIODICIDAD

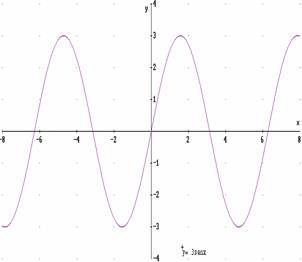
Hablaremos de funciones periódicas cuando sus gráficas se repitan exactamente varias veces.

Diremos que una función es periódica y de periodo k, si la imagen de cualquier valor x coincide con la imagen del valor x + k.

Como ejemplo, tenemos la función seno, que ya la hemos visto antes.

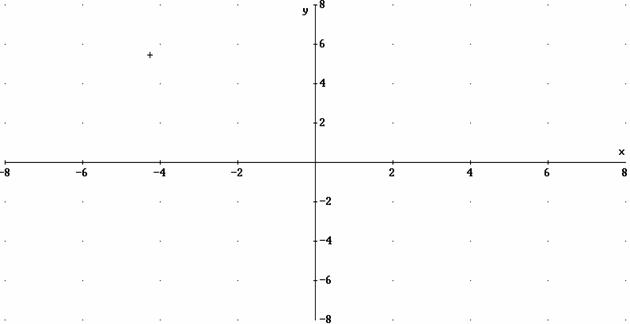
1.- Representa en el siguiente eje de coordenadas una función que sea periódica.

Antonio Romero Luque                                              IES Nuestra Señora de la Victoria

Enero 2005

© Ministerio de Educación, Política Social y Deporte. Año 2005