f(x) = 6 f(x) = − 4 f(x) = 1/7
f(x) =
![]()
son ejemplos de funciones constantes.
FUNCIONES CONSTANTES, LINEALES Y AFINES. RECTAS
ENUNCIADO
Las funciones cuyas gráficas son rectas son:
f(x) = 6 f(x) = − 4 f(x) = 1/7
f(x) =
![]()
son ejemplos de funciones constantes.
f(x)
= − 4x f(x) = 6.5x
f(x) =
![]() f(x) = x
f(x) = x
son funciones lineales.
f(x)
=
![]() f(x) = 3x − 67 f(x) =
f(x) = 3x − 67 f(x) =
![]() f(x) = x + 0.56
f(x) = x + 0.56
son funciones afines.
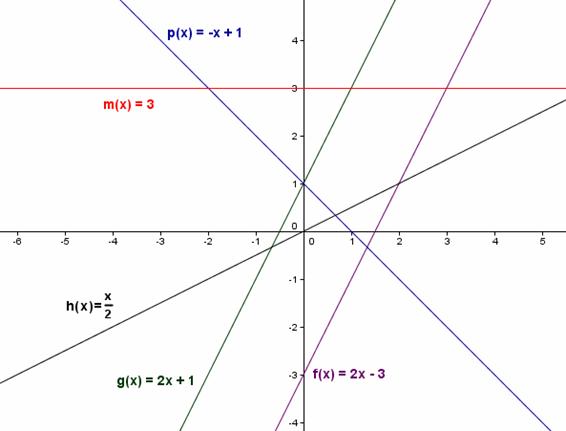
El procedimiento “manual” para dibujar este tipo de gráficas es representar los puntos que se obtienen a partir de una tabla de valores y unirlos mediante un trazo rectilíneo.
Por ejemplo, si queremos dibujar la gráfica de la función f(x) = 2x − 3, en primer lugar, construimos una tabla (sería suficiente con dos valores, pues una recta está determinada por dos puntos).
| x |
y = 2x − 3 |
| 0 |
−3 |
| 2 |
1 |
A continuación dibujamos los puntos (0, −3) y (2, 1) en unos ejes de coordenadas y los unimos mediante un segmento.
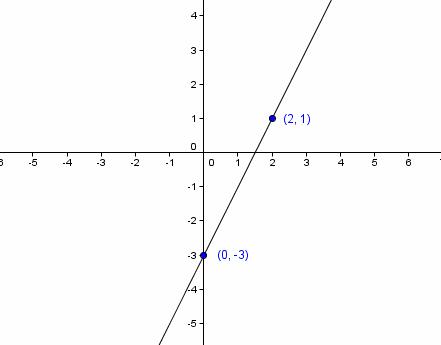
Uno de los objetivos de esta práctica será el proceso inverso: a partir de la gráfica construir una tabla de valores.
Otro objetivo fundamental es el análisis e interpretación gráfica de los coeficientes a y b en la expresión general f(x) = ax + b. El coeficiente a es la pendiente de la recta y b es la ordenada en el origen.
Por último, comenzaréis a usar GeoGebra para dibujar rectas.
QUÉ HACER
Para estudiar las gráficas de funciones constantes el deslizador a deberá tomar el valor 0; en la fórmula de estas funciones no hay x. Para las lineales será b el que sea igual a cero (siendo a ≠ 0). En las funciones afines los parámetros a y b y sus deslizadores serán distintos de cero.
Si quieres construir una tabla de valores sólo tienes que desplazar el punto sobre la gráfica y anotar sus coordenadas en la tabla. Para mover un punto sitúate sobre el y arrástralo manteniendo pulsado el botón izquierdo del ratón.
La respuesta a las preguntas las anotarás en la Ficha del alumno.
En la segunda escena dibujarás las rectas utilizando algunos botones de la Barra de Herramientas o escribiendo la fórmula en la Barra de Entradas. Las construcciones las guardarás con los nombres que se indican.
En la siguiente imagen tienes la pantalla general de trabajo de GeoGebra. Cuando ejecutas el programa ves esta pantalla. Sin embargo, al trabajar en las distintas escenas de esta actividad la pantalla de trabajo será diferente
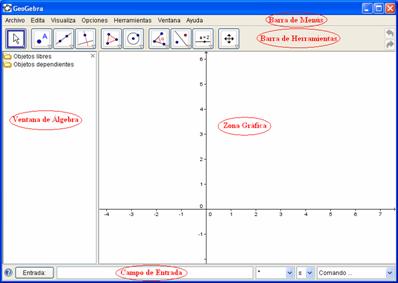
PREGUNTAS
Funciones constantes (y = b → a = 0)
En todo este apartado el deslizador a debe mantenerse
en el valor 0
1.- Sitúa el deslizador a en el valor 0 y mueve lentamente el deslizador b.
- ¿Cómo son todas las gráficas?
-¿Qué caracteriza a las gráficas de las funciones constantes?
2.- Fija el deslizador b
en el valor 4. La recta dibujada es y = 4. Escribe las coordenadas
de tres puntos de la función. Sólo tienes que desplazar el punto
A y fijarte en sus coordenadas.
- ¿Cuáles son
las coordenadas de los tres puntos?
- Sitúa b
en el valor -1 para trazar la gráfica de y = -1 y después
escribe las coordenadas de tres puntos diferentes.
- Si la ecuación de la recta es y = k ¿cuáles
son las coordenadas de un punto genérico de la función?
3.- Sitúa el deslizador b sobre el valor 0 y mueve el deslizador a.
- Todas las gráficas pasan por un mismo punto. ¿Cuál es este punto?
4.- Ve moviendo el deslizador a
de manera que tome únicamente valores positivos: a =
0.8, a = 1, a = 1.25, a =
2, a = 3.1.
- ¿Cómo son
las gráficas cuando a es positivo, crecientes o decrecientes?
5.- Mueve ahora a
de manera que tome valores negativos: a = -0.6, a
= -1, a = -1.8, a = -3.5.
- ¿Cómo son las gráficas cuando a es negativo, crecientes
o decrecientes?
6.- Sitúa ahora el deslizador a en 1.25 y haz una tabla de tres valores de la función moviendo el punto A por la gráfica. Cada vez que muevas A obtendrás un punto de la tabla.
Interpretación geométrica de la pendiente
7.- Sitúa el deslizador a
en 2 y anota las coordenadas de tres puntos (x1, y1),
(x2, y2), (x3, y3)
- (x1, y1)
= ( , )
(x2, y2) = ( ,
) (x3,
y3) = ( , )
- Sustituye las letras por
sus valores y calcula el valor de cada fracción.
(y2-y1)/(x2-x1)
= (y3-y2)/(x3-x2)
=
- ¿Qué valor
se obtiene en ambos casos?
8.- Mueve a situándolo
en -3 y repite los mismos pasos que en la pregunta 6.
- (x1, y1) = ( ,
)
(x2, y2) = ( ,
) (x3,
y3) = ( , )
- (y2-y1)/(x2-x1)
= (y3-y2)/(x3-x2)
=
- ¿Qué valor
tiene la fracción en los dos casos?
9.- Conclusión.
- ¿Podrías explicar
cuál es el significado geométrico de la pendiente de una recta?
Funciones
afines ( y = ax + b)
En este apartado a y b deben
tomar valores distintos de 0
10.- Fija a en
el valor que quieras y después mueve el deslizador b.
- ¿Cómo varían
las rectas cuando cambias el valor de b?
- Todas las rectas tienen la misma pendiente porque no estás moviendo
a ¿Qué tienen en común las rectas cuando
tienen la misma pendiente?
11.- ¿Cómo puedes saber si dos rectas son paralelas a partir de la fórmula de sus ecuaciones?
12.- Fija ahora b
y, sin moverlo, cambia el valor de a.
- Las rectas siempre pasan
por el mismo punto ¿cuáles son sus coordenadas?
- ¿Cuál
es entonces la interpretación gráfica de b?
Interpretación geométrica de la pendiente
13.- Sitúa a
en -2 y determina las coordenadas de tres puntos de la recta moviendo el punto
A.
- (x1, y1)
= ( , )
(x2, y2) = ( ,
) (x3,
y3) = ( , )
- (y2-y1)/(x2-x1)
= (y3-y2)/(x3-x2)
=
- ¿Cuál es el valor
del cociente incremental?
14.- Fija a en
2.5 y vuelve a realizar el mismo proceso.
- (x1, y1)
= ( , )
(x2, y2) = ( ,
) (x3,
y3) = ( , )
- (y2-y1)/(x2-x1)
= (y3-y2)/(x3-x2)
=
- ¿Cuál es el valor
de las dos fracciones?
15.- Conclusión.
- ¿Puedes explicar
cuál es el significado geométrico de la pendiente?
1.- Dibuja la recta que pasa por dos puntos cualesquiera de la pantalla.
![]() y haz clic en dos puntos de la Ventana Gráfica.
y haz clic en dos puntos de la Ventana Gráfica.
b)
Activa Recta que pasa por Dos puntos
![]() y haz clic en los dos puntos que has dibujado
previamente.
y haz clic en los dos puntos que has dibujado
previamente.
c) Guarda la construcción con el nombre recta1.
2.- Dibuja la recta que pasa por los puntos (0,3) y (1,-1).
b) Dibuja la recta que pasa por los dos puntos anteriores.
c) Guarda la construcción con el nombre recta2.
3.- Dibuja la recta f(x) = 2x − 1.
b) Guarda la construcción con el nombre recta3.
Si quieres dibujar la gráfica de una función constante, por ejemplo y = 5, tienes que escribir en el Campo de Entrada y = 5. Si escribes sólo el número 5 el programa no entiende que se trate de una función.
4.- Cambia el color y otras propiedades de objetos dibujados.
Si te sitúas sobre un objeto de
c) Haz que se vea la expresión algebraica de la recta y cambia su color. Ventana Propiedades, pestaña Básico activar Muestra Rótulo / Valor. El color se cambia desde la pestaña Color.
d) Guarda la construcción con el nombre recta4.