FUNCIONES RADICALES
ENUNCIADO
Las funciones radicales son aquellas en las que la variable se
encuentra bajo el signo radical. En esta práctica estudiaremos las funciones
del tipo![]() y también las que tienen como expresión general
y también las que tienen como expresión general ![]() .
.
La gráfica de estas funciones es muy diferente a las de las anteriormente estudiadas.
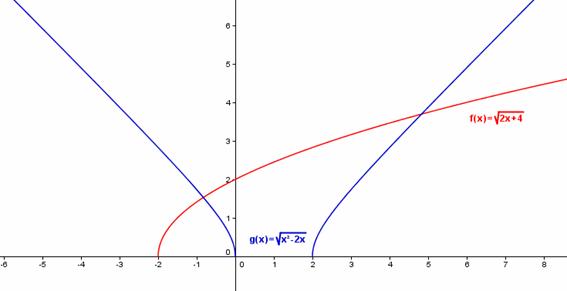
En primer lugar, son funciones positivas, pues en la definición de la función se considera únicamente la raíz positiva del radicando.
(Si la expresión algebraica de la
función fuera ![]() entonces serían funciones que sólo tomarían valores
negativos)
entonces serían funciones que sólo tomarían valores
negativos)
En segundo lugar, si observas las gráficas representadas podrás ver que, en muchas ocasiones, sólo están definidas en un tramo de la recta real; en estos casos su dominio de definición no son todos los números reales ya que la raíz cuadrada sólo está definida para valores positivos del radicando.
Por último, su comportamiento respecto a la monotonía (crecimiento y decrecimiento) es bastante sencillo.
En esta práctica vamos a estudiar
las propiedades fundamentales de los dos tipos de funciones radicales: ![]() y
y ![]() .
.
QUÉ HACER
En la primera escena puedes ver la
gráfica de la función ![]() para los valores en
los que estén situados los deslizadores.
para los valores en
los que estén situados los deslizadores.
En primer lugar analizarás las
propiedades de las funciones del tipo ![]() , para lo que situarás el deslizador a en el valor 0. Moviendo los otros deslizadores estudiarás:
, para lo que situarás el deslizador a en el valor 0. Moviendo los otros deslizadores estudiarás:
– El dominio de definición de la función.
– El crecimiento o decrecimiento de la misma.
– La existencia de extremos relativos (máximos y mínimos).
Después estudiarás estas
propiedades para las funciones del tipo ![]() situando el deslizador
a en valores no nulos.
situando el deslizador
a en valores no nulos.
PREGUNTAS
Funciones radicales. Escena 1
Empezamos con el estudio de las
funciones radicales del tipo
![]() por lo que el deslizador a debe permanecer en el valor 0.
por lo que el deslizador a debe permanecer en el valor 0.
Mueve después b y c. Verás que todas las gráficas son muy similares.
1.- Sin mover c
observa el trazado de las gráficas para los siguientes valores positivos
de b:
b = 0.4
b = 1
b = 2.5
b = 4.6
- Para valores positivos de b ¿cómo son las
funciones, crecientes o decrecientes?
2.- Veamos ahora el caso de los valores negativos de b.
Fíjate en la gráfica para:
b = -0.1 b
= -1.3 b
= -2 b
= -3.9
- Para valores negativos de b ¿las funciones son crecientes
o decrecientes?
3.- Este tipo de funciones radicales sólo tienen un extremo.
- ¿Qué es, máximo o mínimo?
- En cada caso escribe las coordenadas del extremo de la función:
y = √ (2x+5)
Extremo: ( ___ , ___ )
y = √ (-3x+4)
Extremo: ( ___ , ___ )
y = √ (4x-16)
Extremo: ( ___ , ___ )
4.- Dominio de definición. Recuerda que el dominio de definición
es el conjunto de valores de x para los que está definida
la función que, gráficamente corresponde, a la parte del eje
X en la que hay función.
- Si b = 1 y c = -3, ¿cuál
es el dominio de definición?
- ¿Cuál es el dominio cuando b = 2 y c
= 4?
- ¿Sabrías expresar el dominio de definición en función
de b y c?
Pasemos al siguiente tipo de función
radical:
![]() . El valor de a ha de ser distinto de cero. Si mueves los
deslizadores verás que este tipo de funciones tienen gráficas muy distintas
a las anteriores.
. El valor de a ha de ser distinto de cero. Si mueves los
deslizadores verás que este tipo de funciones tienen gráficas muy distintas
a las anteriores.
5.- a > 0. Fija el deslizador a en un valor positivo y después mueve b y c. Verás que las gráficas son similares.
6.- Fija los deslizadores en los valores a =1, b
= 0, c =1 y responde:
- La función es simétrica. ¿Cuál es su eje de
simetría?
- ¿Cuál es su dominio de definición?
- ¿Tiene algún máximo o mínimo? ¿Dónde
se encuentra/n? (escribe sus coordenadas)
Fija a = 2.5 , b = 1, c
= - 2.
- Eje de simetría.
- Dominio de definición.
- Coordenadas de extremos relativos.
7.- a < 0. Sitúa a en un valor negativo y luego mueve b y c. Todas las gráficas son parecidas, pero son muy diferentes al caso anterior, cuando a > 0.
8.- Mueve los deslizadores a los valores a = -1, b
= 0, c = 4 y responde:
- ¿Cuál es el eje de simetría de la función?
- ¿Cuál es su dominio de definición?
- ¿Tiene algún máximo o mínimo? ¿Cuáles
son sus coordenadas?
Cambia el valor de a = - 2, b = 4, c
= 0.
- Eje de simetría.
- Dominio de definición.
- Coordenadas de extremos relativos.
Funciones radicales. Escena 2
1.- Con ayuda de la gráfica de las funciones vas a contestar a las siguientes preguntas:
- la raíz cuadrada de un número, ¿es menor o mayor que el número?
- el cuadrado de un número, ¿es menor o mayor que el número?
a)
Con la rueda del ratón y con el botón Desplazar Vista
Gráfica ![]() amplía el zoom de manera que el eje vertical
esté entre -1.5 y 3, aproximadamente.
amplía el zoom de manera que el eje vertical
esté entre -1.5 y 3, aproximadamente.
b)
Dibuja las gráficas de las funciones f(x) = x,
g(x) = x2,
![]() . Para introducir la fórmula de
. Para introducir la fórmula de
![]() debes escribir h(x) = sqrt(x)
debes escribir h(x) = sqrt(x)
c) Cambia el color de las gráficas.
d)
Ordena las funciones f(x) = x, g(x)
= x2,
![]() en el intervalo [0 , 1].
en el intervalo [0 , 1].
e)
Ordena las funciones f(x) = x, g(x)
= x2,
![]() en el intervalo [1 , +∞).
en el intervalo [1 , +∞).
f) ¿Es siempre menor un número que su cuadrado?
g) ¿Es siempre mayor un número que su raíz cuadrada?