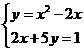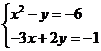Hemos visto en la práctica anterior
que las gráficas de las funciones con fórmulas más sencillas (constantes,
lineales y afines) eran rectas. Ahora estudiaremos las gráficas de las siguientes
funciones en cuanto a la complejidad de su expresión algebraica: las funciones
cuadráticas: f(x) = ax2
+ bx + c. Su representación gráfica no puede ser una recta;
es una curva llamada parábola.
Se trata de una curva muy común y bien conocida. De hecho estás rodeado de
fragmentos de parábolas, aunque no te hayas dado cuenta. No tienes más que
mirar las antenas parabólicas de los tejados y balcones o
seguir la trayectoria de un balón cuando lo golpeas.
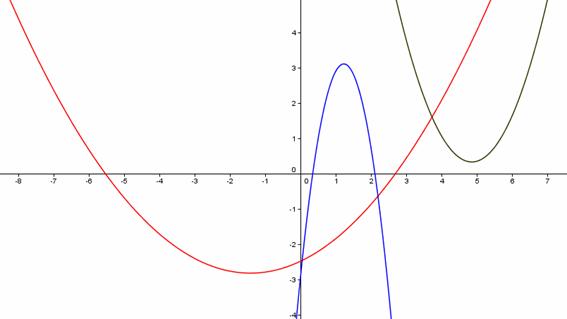
Recuerda que el trazado manual
de una parábola conlleva cierto trabajo. Si intentas dibujar la gráfica a
partir de una tabla de valores elegidos al azar el resultado puede ser parcial,
no dar información de la parte crítica de la gráfica. Hay que calcular los
puntos de corte con el eje OX (si es que existen) resolviendo la ecuación
de segundo grado ax2 + bx + c = 0. Además,
hay que calcular las coordenadas del vértice, el punto más importante, que
se puede hacer a partir de los cortes con el eje horizontal o mediante una
fórmula. Por último es recomendable completar una tabla de valores con puntos
cercanos a los anteriores … y después representarlos en unos ejes de coordenadas
y unirlos con el mejor trazo posible para que obtener lo más aproximado a
una parábola.
En esta práctica tendremos la
gráfica ya dibujada. Uno de los objetivos es analizar la relación entre el
valor de los coeficientes a, b y c
y las propiedades de la gráfica. También investigarás cuáles son las coordenadas
del vértice y qué relación tienen estas coordenadas con los coeficientes de
la función
Por último, y siguiendo en la
iniciación de construcciones propias, resolverás gráficamente sistemas de
ecuaciones lineales y no lineales.
1.- Mueve todos los deslizadores
y observa cuál es el efecto del cambio de cada deslizador en el trazado
de la gráfica.
2.- La línea discontinua
no forma parte de la gráfica pero es su eje de simetría. Si, idealmente,
doblaras la gráfica por esta línea cada rama de la parábola
quedaría superpuesta en la otra rama.
- ¿Cómo se llama
el punto de intersección del eje de simetría con la parábola?
Interpretación geométrica
del coeficiente x2 (a)
3.- Sitúa el deslizador en
a = 1.
- La gráfica ¿qué
tiene, máximo o mínimo?
- ¿Cómo se llama
el punto en el que se alcanza el máximo / mínimo?
- ¿Cuál es la
curvatura de la gráfica, cóncava hacia arriba (forma de U) o cóncava
hacia abajo (forma de ∩)?
4.- Fija a en 1.75.
- ¿Hay máximo
o mínimo?
- ¿Cuál es el
punto donde se alcanza el máximo / mínimo?
- ¿Cómo es la
concavidad de la gráfica, cóncava hacia arriba (forma de U) o
cóncava hacia abajo (forma de ∩)?
5.- Mueve a al
valor 3.
- El extremo de la función,
¿es un máximo o un mínimo?
- ¿Dónde está
el máximo / mínimo?
- ¿Cómo es la
concavidad de la gráfica?
6.- Has visto el trazado de la
curva para los valores de a iguales a 1, 1.75 y 3, todos ellos
valores positivos. Mueve el deslizador de forma que tome otros valores positivos
y piensa en la respuesta a las tres preguntas que se han hecho en cada caso.
7.- Conclusión.
Si el coeficiente de x2
(a) es positivo, el vértice es un __________ y la gráfica
es cóncava hacia _________.
Veamos qué ocurre cuando
a toma valores negativos.
8.- Sitúa el deslizador en
a = –2.
- El vértice ¿es
un máximo o un mínimo?
- ¿Cuál es la
curvatura de la gráfica, cóncava hacia arriba (forma de U) o cóncava
hacia abajo (forma de ∩)?
9.- Mueve a al
valor –0.5.
- El vértice ¿es
el máximo o el mínimo?
- ¿Cuál es la
curvatura de la gráfica?
10.- Conclusión. Cambia
el deslizador para otros valores negativos y fíjate en su trazado respecto
a la existencia de máximo o mínimo y en cuanto a su curvatura.
Si el coeficiente de x2
(a) es negativo, el vértice es un __________ y la gráfica
es cóncava hacia _________.
11.- Seamos más precisos.
- Mueve lentamente a desde 0.1 hasta 4.5 ¿Cómo
varía el trazado de la parábola en función de la magnitud
de a?
- Repite el proceso para valores
de a negativos. Desliza lentamente a desde
–5 hasta –0.1. ¿Cuál es el cambio en la gráfica cuando
a, en valor absoluto, se va haciendo más pequeño?
Interpretación geométrica
del término independiente (c)
12.- Mueve los deslizadores a,
b y c a los valores 1, 0 y 0 respectivamente.
La gráfica en pantalla es la de f(x) = x2.
Cambia el valor de c de manera que tome valores positivos y
negativos.
- ¿Cuál es el efecto de la variación de c en
el trazado de la gráfica?
- Sitúa a
= -1 y b = 2. Después cambia el valor de c
y observa el efecto de los cambios en el trazado de la gráfica. ¿Puedes
formular una interpretación gráfica del coeficiente c?
a y b.
13 .- Fija ahora a
= - 0.5 y c = 3 y después modifica b.
- ¿Varía la curvatura o la amplitud de la parábola?
Coordenadas del vértice
14.- Estudiemos
ahora cómo determinar las coordenadas del vértice.
a) Fija los deslizadores en a
= 0.5, b = −1, c = −4. Si no puedes fijar algún valor
exacto “a pulso” sitúate sobre el deslizador correspondiente, ve a Propiedades
pulsando el botón derecho y en la pestaña Básico teclea el número que corresponda
en Valor.
Recuerda que activando Desplazar
Vista Gráfica 
puedes mover la
pantalla para que se vea la parte de la gráfica que te interese.
b) Despliega el botón Puntos,
selecciona Intersección de Dos Objetos
, haz clic sobre el eje OX y después sobre la gráfica y se verán
los puntos de corte de la parábola y el eje OX.
c) Desde Propiedades
haz que se vean las coordenadas de los dos puntos de corte (Propiedades /
Básico / Muestra Rótulo / Valor).
d) ¿Qué relación hay
entre la coordenada x del vértice
y la de los puntos de corte con el eje horizontal? Para responder fíjate en
la simetría de la gráfica y en el valor numérico de las coordenadas respectivas.
e) Mueve los deslizadores de manera
que la parábola siempre corte al eje horizontal y comprueba que la relación
entre las coordenadas x de los puntos
de corte y la del vértice es siempre la misma.
Recuerda que para hallar los puntos
de corte con el eje OX (y = 0) se
resuelve la ecuación ax2 + bx + c =
0. Las soluciones vienen dadas por
las expresiones
Por otra parte sabemos que el
punto medio entre dos puntos es la media de sus valores numéricos (el punto
medio entre 3 y 9 es 6, que se obtiene calculando (3+9) / 2 , entre −1
y 8 es 3.5, resultado de efectuar (−1+8) /2 )
Así pues, lo que tienes
que hacer es sumar las expresiones de x1 y x2
y dividir el resultado entre 2.
15.- Conclusión: ¿cuál es fórmula
de la coordenada x del vértice?
Esta fórmula es válida aunque
la parábola no corte al eje OX.
Resolución
gráfica de sistemas de ecuaciones
Abre un archivo nuevo
desde la Barra de Menús, Archivo / Nuevo.
1.- Resuelve gráficamente el sistema
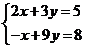
a)
Escribe en el Campo de Entrada las ecuaciones que componen el sistema.
b)
Cambia el color de las gráficas y haz que se vea su fórmula (botón
derecho / Muestra Rótulo).
c)
Con la herramienta Intersección de Dos Objetos
marca el punto de corte.
d)
Desde Propiedades haz visible sus coordenadas (botón derecho / Propiedades
/ pestaña Básico / activa Muestra Rótulo seleccionando
Nombre y Valor).
e)
Solución:
x
= ______ y
= ______
2.- Resuelve gráficamente el sistema
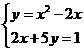
a)
Repite el proceso del anterior ejercicio.
x
= ______ y
= ______
El exponente
2 lo puedes introducir como en una Hoja de Cálculo (^2) o insertando el superíndice
2 desde la primera barra despegable del Campo de Entrada.
Si quieres
aumentar el zoom de la Ventana Gráfica haz clic sobre Desplazar Vista Gráfica
, pincha después en la pantalla y mueve la rueda
del ratón. (Si arrastras el puntero verás cómo se desplaza la vista gráfica)
3.- Resuelve gráficamente el sistema
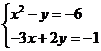
x
= ______ y
= ______