FUNCIONES DE PROPORCIONALIDAD INVERSA. HIPÉRBOLAS
ENUNCIADO
El siguiente tipo de funciones
que vamos a estudiar son las de proporcionalidad
inversa, las funciones en cuya expresión algebraica aparece x con exponente 1 en el denominador. Sus
gráficas, que no pueden ser rectas, son curvas llamadas hipérbolas. La expresión general de este tipo de funciones es 
, donde a, b, c
y d son números reales.
Son funciones de proporcionalidad inversa:
Las gráficas de estas funciones son las de la imagen. Observa que la gráfica de una función de proporcionalidad inversa tiene dos ramas.
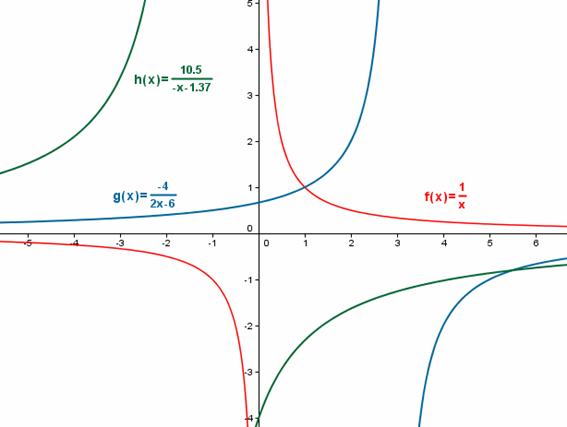
El trazado “manual” consiste en hacer una tabla de valores de puntos para las dos ramas de la hipérbola. Para hacer la tabla razonablemente se deben identificar dos rectas que no forman parte de la gráfica, pero que dan información esencial sobre ella.
Una es la recta paralela al eje OY que separa las dos ramas y a la que se acercan estas “tanto como uno quiera”; es la asíntota vertical. Está muy relacionada con el punto que se excluye del dominio de definición. La otra es la recta paralela al eje OX a la que se aproxima la gráfica por la derecha y por la izquierda, cuando el valor absoluto de la variable es “grande”; esta recta es la asíntota horizontal.
En esta práctica vamos a estudiar las propiedades de las funciones de proporcionalidad inversa y el significado geométrico de los coeficientes a, b, c y d.
Nos detendremos también en el análisis del dominio de definición de estas funciones. Recuerda que el dominio de definición de una función es el conjunto de números reales para los que está definida la función.
El dominio de las funciones lineales y cuadráticas es el conjunto de todos los números reales; cualquier número real tiene su imagen, en la definición de las funciones no hay operaciones que puedan presentar “problemas”.
Por último, y siguiendo con las construcciones propias de GeoGebra, resolveremos sistemas en los que una de las ecuaciones corresponda a una función de proporcionalidad inversa.
QUÉ HACER
En la primera escena puedes ver la
gráfica de la función para los valores en
los que estén situados los deslizadores
horizontales. También se pueden ver en trazo discontinuo las gráficas de las
dos asíntotas, la vertical y la horizontal.
Como en prácticas anteriores, al mover los deslizadores se cambian los valores de los coeficientes; el trazado de la gráfica se adapta dinámicamente a los nuevos valores.
Trazarás varias gráficas situando los deslizadores en los valores que se indiquen. En cada caso estudiarás:
- Los puntos de corte con los ejes.
- El dominio de definición.
- El crecimiento o decrecimiento de la función. .
- Las ecuaciones de las asíntotas.
En la segunda escena seguirás trabajando en la resolución gráfica de sistemas de ecuaciones.
PREGUNTAS
Funciones de proporcionalidad inversa. Escena 1
Mueve todos los deslizadores lentamente. Verás que el más “sensible” respecto al trazado de la gráfica es b. Si quieres un deslizamiento más fino haz clic sobre el punto del deslizador. Cuando aparezca una cruz en lugar del puntero muévete con las teclas de desplazamiento de cursor manteniendo pulsada la tecla Mayúsculas.
Veamos algunos ejemplos.
1.- Dibuja la gráfica de la función f(x) =
2 / (x - 5) . Para ello tendrás que situar los deslizadores
en los valores a = 2, b = 1, c
= -5, d = 0.
- ¿Cuál es su dominio de definición?
- ¿Cuáles son los puntos de corte con los ejes de coordenadas?
- En los intervalos que está definida, ¿es creciente o decreciente?
Hay un punto en el eje X cerca del cuál la gráfica se “dispara”
porque los valores de la función se hacen tan grandes como uno quiera
si nos acercamos lo suficiente a ese punto. Ese punto determina la asíntota
vertical.
- ¿Cuáles son las coordenadas de ese punto?
- ¿Cuál es la ecuación de la asíntota vertical?
- En estas funciones, ¿qué relación hay entre el dominio
de definición y la asíntota vertical?
En la gráfica de la función puedes ver que cuando x se hace grande en valor absoluto (a la derecha y a la izquierda de la gráfica) su trazado se acerca a otra recta, en este caso horizontal. Es la asíntota horizontal. Su ecuación es y = 0, que es precisamente el valor del parámetro d.
2.- Dibuja la gráfica de la función f(x) =
1- 3 / (2x + 8) (a
= -3, b = 2, c = 8, d = 1)
- ¿Cuál es su dominio de definición?
- ¿Cuáles son los puntos de corte con los ejes de coordenadas?
- En los intervalos que está definida, ¿es creciente o decreciente?
- ¿Cuál es la ecuación de la asíntota vertical?
- ¿Cuál es la ecuación de la asíntota horizontal?
3.- Dibuja la gráfica de la función f(x) = (4x
+ 1) / ( 2x + 3)
Lo primero que tienes que hacer es expresar la función en la forma general,,
para lo que tendrás que hacer, con papel y lápiz, la división
entera del numerador entre el denominador para hallar el cociente y resto:
d es el cociente y a el resto.
- Una vez hecha la división entera, ¿cuáles son los valores
de los parámetros?
a = ___ b
= ___ c = ___ d
= ___
- ¿Cuál es su dominio de definición?
- ¿Cuáles son los puntos de corte con los ejes de coordenadas?
- En los intervalos que está definida la función, ¿es creciente
o decreciente?
- ¿Cuál es la ecuación de la asíntota vertical?
- ¿Cuál es la ecuación de la asíntota horizontal?
4.- Dibuja la gráfica de f(x) = (x - 6) /
(4x - 9) y responde a las siguientes cuestiones:
- Dominio de definición:
- Coordenadas de los puntos de corte con los ejes:
- En los intervalos que está definida, ¿es creciente o decreciente?
- Ecuación de la asíntota vertical:
- Ecuación de la asíntota horizontal:
Si
entonces:
- Los puntos de corte con los ejes
son:
- El dominio de definición es:
- ¿Qué relación hay entre el dominio de definición
y la asíntota vertical?
- Asíntota vertical: x =
- Asíntota horizontal: y =
Funciones de proporcionalidad inversa. Escena 2
1.- Resuelve gráficamente el sistema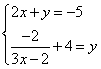
a) Dibuja la gráfica de las dos funciones en distintos colores y de manera que se vea la fórmula de cada una.
¡Atención! En el Campo de Entrada hay que escribir la expresión despejada sólo dependiente de x. Es decir, en cada ecuación hay que despejar la variable y para escribir únicamente la expresión despejada en la que aparece la variable x. Por ejemplo, en la primera ecuación al despejar y se obtiene y = - 2x - 5. En el Campo de Entrada hay que escribir únicamente - 2x - 5.
b) ¿Cuántas soluciones hay?
c)
Con la herramienta Intersección de Dos Objetos
marca todos los puntos de corte.
d) Desde Propiedades haz visible sus coordenadas.
e) Guarda la construcción con el nombre inversa1.
f) Solución:
2.- Resuelve gráficamente el sistema
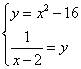
a) Repite el proceso del anterior ejercicio.
b) Guarda la construcción con el nombre inversa2.
c) Solución: