La expresión general de una función
exponencial es f(x) = ax donde
a es un número real positivo y distinto de 1 llamado base
de la función.
El trazado “manual” de las gráficas
de estas funciones se hace a partir de una tabla de valores que se construye
con ayuda de la calculadora científica con la función xy
o ^, dependiendo del
modelo. En esta tabla puede ser conveniente dar valores decimales a la variable
porque si nos limitamos a valores enteros la función puede por una parte
crecer y por otra, acercarse a cero en un intervalo muy pequeño.
En el dibujo puedes ver las gráficas
de las funciones 0.7x, 0.15x, 10x
y 2x.
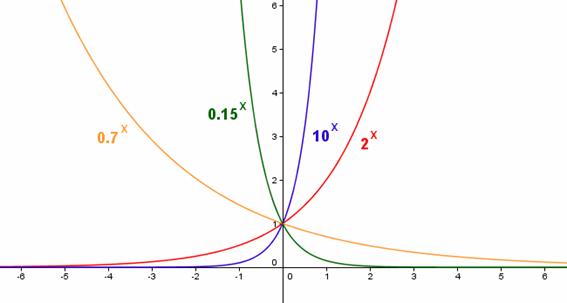
Observa, en primer lugar, que
todas las funciones son positivas. Además, todas cortan al eje OY en el mismo
punto. Por otra parte, parece haber dos tipos de gráficas: las que tienen
las de base menor que 1, por un lado, y las que tienen base mayor que 1, por
otro.
En esta práctica uno de los objetivos
es precisar estas similitudes y llegar a enunciar las propiedades fundamentales
de este tipo de funciones.
El estudio de las funciones exponenciales
va a ir acompañado del estudio de las funciones logarítmicas pues ambas funciones guardan
una íntima relación al ser inversas; la función inversa de la función exponencial
es la logarítmica de la misma base, y la inversa de la función logarítmica
es la exponencial.
Veamos
qué son funciones inversas con un ejemplo.
5;
f(5) = 4·5 = 20 ; g(20) = 20/4 = 5
13; f(13) = 4·13 = 52 ; g(52) = 52/4 = 13
(La propiedad también es válida si aplicamos las funciones
en orden inverso, primero dividiendo por cuatro el número y después multiplicando por cuatro el resultado)
Recordemos la definición del logaritmo de un número, que se hace en términos
de la función exponencial.
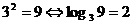 (el logaritmo
en base 3 de 9 es igual a 2)
(el logaritmo
en base 3 de 9 es igual a 2)
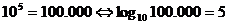 (el logaritmo
en base 10 de 100.000 es 5)
(el logaritmo
en base 10 de 100.000 es 5)
En general, el logaritmo en base a de b (se escribe
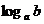 ) es el exponente al que hay que elevar a para obtener b.
) es el exponente al que hay que elevar a para obtener b.
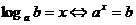
Una consecuencia de la definición
del logaritmo es que la base tiene que ser un número positivo, al igual que
en las funciones exponenciales.
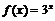 y
y
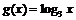 son funciones inversas: si elevamos
3 a un número cualquiera (x) y después calculamos el logaritmo en base 3 del valor obtenido
tenemos el número inicial (x):
son funciones inversas: si elevamos
3 a un número cualquiera (x) y después calculamos el logaritmo en base 3 del valor obtenido
tenemos el número inicial (x):
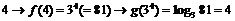
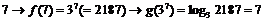
(Como
antes, si componemos en orden inverso las funciones, primero calculamos el
logaritmo y después la exponencial de la misma base, volvemos al valor inicial)
Si se conoce
el valor de los logaritmos en una base determinada y las propiedades generales
de los logaritmos se pueden calcular logaritmos en cualquier base. Con ayuda
de la calculadora podemos calcular los logaritmos de base 10, llamados logaritmos decimales, y los de base e, que son los logaritmos neperianos. Las funciones son log para logaritmos decimales,
y ln para logaritmos neperianos.
El trazado manual de una función
logarítmica de base distinta a 10 ó e
requiere, por tanto, el conocimiento de las propiedades de los logaritmos.
(Este número e aún no lo conocéis, pero es uno de los números más importantes en
las matemáticas. Su expresión decimal aproximada es e ≈ 2.7182818…)
Las siguientes gráficas son de
funciones logarítmicas.
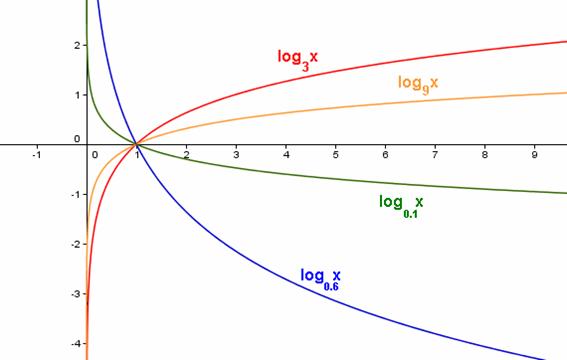
Si las observas detenidamente
verás que, girándolas, se parecen mucho a las de las funciones exponenciales.
La razón es que exponenciales y logarítmicas son funciones inversas, al igual
que las funciones "multiplicar por cuatro" y "dividir por cuatro".
Con ayuda de GeoGebra
se pueden estudiar las propiedades generales de las funciones logarítmicas.
En la escena de GeoGebra puedes ver el trazado de la función f(x)
= ax para
el valor actual del deslizador, es decir, puedes ver el trazado de f(x)
= 2x. Moviendo este deslizador, en la parte superior izquierda,
cambia la base de la función y su trazado.
En la parte superior derecha hay
dos deslizadores, Exp y Log,
que funcionan como interruptores. Cuando el deslizador está en el valor 1
se ve la función correspondiente; cuando está en el valor 0 la gráfica no
se ve en pantalla.
En la primera parte de la tarea
estudiarás las propiedades de la función exponencial distinguiendo los casos
en que la base de la función es mayor y menor que 1.
Después, cambiando las posiciones
de los interruptores, analizarás las principales de las funciones logarítmicas.
Por último, relacionarás ambas
funciones a partir de los trazados de sus gráficas.
El deslizador a, en la parte superior izquierda
debe estar en el valor 2. Los interruptores de la parte superior derecha tienen
que estar en las posiciones Exp = 1,
Log = 0. En pantalla se ve únicamente la gráfica de f(x)
= 2x . Si no es así sitúa los deslizadores e interruptores
en las posiciones indicadas.
1.- Mueve el deslizador a en un rango de valores mayores que 1
y responde a las siguientes preguntas:
–
¿Cuál es el dominio de la función?
–
¿Qué signo tiene la función en todo su dominio?
–
Todas las gráficas pasan por un punto ¿Cuál es? ¿Por qué todas pasan por ese
punto?
–
Para valores de la base mayores que 1, ¿cómo son las funciones, crecientes
o decrecientes?
–
¿Tienen algún máximo o mínimo? ¿Dónde?
–
Cuando la variable x se hace grande y positiva, ¿cómo se comporta la función?
–
Asíntota horizontal por la izquierda. Cuando x es negativa y grande en valor absoluto,
¿hacia dónde se acerca la función?
2.- Ahora estudiaremos las propiedades
de las funciones exponenciales de base comprendida entre 0 y 1. Mueve el deslizador
a en un rango de valores menores
que 1 y responde a las siguientes preguntas:
–
¿Cuál es el dominio de la función
–
¿Qué signo tiene la función en todo su dominio?
–
Todas las gráficas pasan por un mismo punto ¿Cuál es? ¿Por qué?
–
Para valores de la base menores que 1, ¿cómo son las funciones, crecientes
o decrecientes?
–
¿Tienen algún máximo o mínimo?
–
Asíntota horizontal por la derecha. Cuando la variable x
se hace grande y positiva, ¿cómo se comporta la función?
–
Para valores de x negativos y grandes en valor absoluto, ¿qué ocurre a la función?
Estudiaremos ahora las propiedades
de las funciones logarítmicas. Cambia los interruptores a los valores Exp
= 0 y Log = 1.
3.- Cálculo de logaritmos a partir de la gráfica.
Sitúa el deslizador a en el valor
2 y moviendo el punto sobre la gráfica calcula los siguientes logaritmos:
log
2 8 = log 2 32 =
log
2 21 = log
2 0.5 =
4.- Mueve el deslizador a en un rango de valores mayores que 1
y responde a las siguientes preguntas:
–
¿Cuál es el dominio de la función?
–
¿En qué intervalo la función es positiva?
–
¿En qué intervalo la función es negativa?
–
Todas las gráficas pasan por un punto ¿Cuál es?
–
Para valores de la base mayores que 1, ¿cómo son las funciones, crecientes
o decrecientes?
–
¿Tienen algún máximo o mínimo? ¿Dónde?
–
Cuando la variable x se hace grande y positiva, ¿cómo se comporta la función?
–
Asíntota vertical por la derecha. Cuando x se acerca al valor 0, ¿qué ocurre con
la gráfica de la función?
5.- Vamos ahora con el estudio
para valores de la base del logaritmo comprendidos entre 0 y 1. Mueve el deslizador
a en un rango de valores menores
que 1 y responde a las siguientes cuestiones:
–
¿Cuál es el dominio de la función?
–
¿En qué intervalo la función es positiva?
–
¿En qué intervalo la función es negativa?
–
Todas las gráficas pasan por un punto ¿Cuál es?
–
Para valores de la base menores que 1, ¿cómo son las funciones, crecientes
o decrecientes?
–
¿Tienen algún máximo o mínimo? ¿Dónde?
–
Cuando la variable x se hace grande y positiva, ¿cómo se comporta la función?
–
Asíntota vertical por la izquierda. Cuando x se acerca al valor 0, ¿qué ocurre con
la gráfica de la función?
Para finalizar veremos la relación
que existe entre las gráficas de la función exponencial y la logarítmica de
la misma base.
Sitúa los interruptores en los
valores Exp = 1
y Log = 1.
6.- Mueve el deslizador a y observa qué ocurre. ¿Cuál es la relación
entre las gráficas de las dos funciones, la exponencial y la logarítmica?

