Funció

	CONCEPTE DE FUNCIÓ
	Anàlisi

1. INTERPRETACIÓ

Fixa't bé en les següents imatges i respon a les preguntes que es formulen en el full de treball

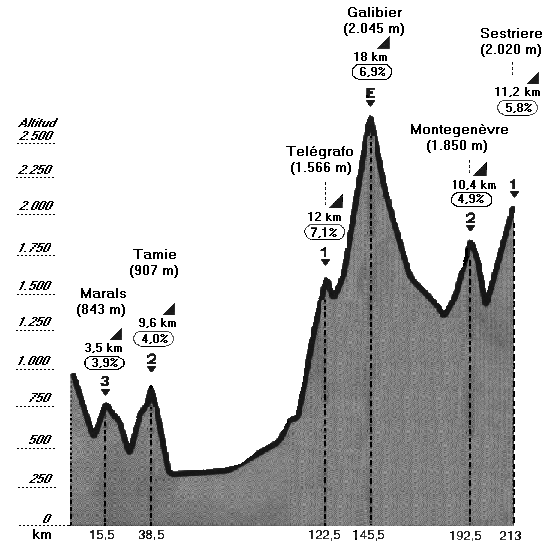QÜESTIONS: La imatge de l'esquerra correspon a la
novena etapa del Tour de França. Observa bé el perfil
de l'etapa i respon a les següents qüestions:

1.a) Quants quilòmetres té en total l'etapa? Per què?

1.b) Quants quilòmetres hi ha en total de pujada?
Com ho has fet?

1.c) I quants hi ha de baixada? Explica-ho.

1.d)En quins punts quilomètrics de l'etapa hi ha els ports
de muntanya? Anota les altituds.
I en quins hi han "les valls"? (aprox.)

1.e) Quin és el port de muntanya amb més altiud?
Quin port de muntanya té major longitud?
I en quin hi ha major pendent? Raona les respostes.

1.f) Podria ser que en el punt quilomètric 122,5 el port de
muntanya Telégrafo tingués dues altituds, p.ex: 1.566 m
i 1.124 m? Raona-ho

1.g) Descriu breument el recorregut de l'etapa a
la vista de les dades que apareixen a la gràfica.

2. CONCEPTE DE FUNCIÓ

Llegeix acuradament les següents situacions i indica si estan relacionades o no. Indica quina de les dues situacions depen de l'altre.

2.a) Velocitat d'un vehicle i distància recorreguda pel mateix

2.b) Edat d'una persona amb la seva alçada.

2.c) La roba d'una persona amb el model de cotxe a comprar.

2.d) Factura de l'aigua d'una casa en un mes i el consum d'aigua de la mateixa casa en el mateix mes.

Per tant:

Una funció és una relació entre dues variables numèriques, habitualment les anomenem x i y; una d'elles rep el nom de variable dependent (la y) doncs el seu valor sempre depén dels valors de l'altra variable; així doncs, l'altra s'anomena variable independent i sol ser la x.

A més a més ha de complir una condició molt important, per cada valor de la variable independent només li pot correspondre un valor (o cap) de la variable dependent. No pot ser que a un valor de la variable independent li corrresponguin dos o més valors de la dependent, si fos així la relació entre les dues variables no és una funció.

ACTIVITAT 1:

Fixa't bé en l'escena de la dreta, hi surten dues gràfiques una de vermella i l'altra verda.

Per poder fer aquesta activitat hauràs d'interactuar amb l'escena de Descartes, per això clica amb el botó esquerra del ratolí el punt P i trasllada'l horitzontalment per l'eix de les abscisses.

Mou el punt P, observa i respon:

a) Què succeeix amb la recta vertical blava?

b) Mentre vas movent el punt P, anota que va succeint amb la recta vertical i les gràfiques de color verd i vermell. Observes res que et cridi l'atenció?

c) Digues quina de les dues gràfiques correspon a una funció i quina no ho és. Raona la teva resposta.

d) Aleshores la recta blava vertical es pot considerar funció? Per què?

e) I si la recta blava fos horitzontal? Raona la resposta

Esta unidad interactiva requiere la máquina virtual de Java J2RE.

	Susanna Igual López

	© Ministerio de Educación. Any 2010. INS F. X. Lluch i Rafecas

Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.