Para estudiar dos funciones lineales a la vez, representamos sobre los mismos ejes las dos rectas. Las coordenadas del punto de corte se hallan resolviendo el sistema formado por las dos ecuaciones . Este punto tiene gran importancia en  el estudio que queramos hacer de las dos funciones.

    Vamos a estudiar en concreto el problema dado con el siguiente enunciado

Empezamos a resolver el problema:  

    Depósito A

 Por los datos del problema sabemos que (0,15) es un punto de la función y que la pendiente es m = -2

 Con esto podemos escribir la ecuación punto-pendiente  y = 15-2x

    Depósito B

  Como el depósito B al principio está vacio el punto (0,0) pertenece a la función que buscamos y la pendiente m = 1

  De esta forma la ecuación de proporcionalidad que lo representa es y = x

    En la primera escena representamos la ecuación obtenida para el depósito A:

    En la segunda representamos la ecuación obtenida para el depósito B:

    En la última escena hacemos la representación conjunta de las dos y contestamos las dos preguntas planteadas en el enunciado. Es decir,  resolvemos el sistema

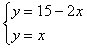
Por tanto los dos depósitos tendrán la misma cantidad de agua cuando pasen 5 minutos desde que se empieza a vaciar el depósito A y a llenar el B y en se momento tendrán 5 litros de agua.

1.- Resuelve en tu cuaderno el siguiente problema: 

El servidor de Internet Ola tiene la tarifa "Primavera", en la cual se paga una cuota fija mensual de 15 € y 0,01 € por cada minuto de conexión. Calcula el gasto, Y, en función de los minutos, x, de utilización de Internet y representa la función Y=f(x).

El Servidor de Internet Marea, tiene la tarifa "Invierno" en la cual no hay cuota fijo sino que tan solo hay que pagar 0,02 € por minuto de conexión. Calcula para esta compañia el gasto, Y', en función del tiempo, x,  en minutos y representa la función Y'=f(x).

Después de tener representadas las dos funciones contesta las siguientes preguntas: ¿Con cuántos minutos de uso pagaremos lo mismo con las dos tarifas? ¿A partir de cuántos minutos es menos rentable "Primavera" que "Invierno"

Puedes utilizar las tres escenas para comprobar tus resultados

2.- Inventa el enunciado de un problema en el que intervengan dos funciones lineales (por ejemplo dos empresa A y B cuyos beneficios vienen dados por y= f(x) ,  y= g(x) respectivamente. Escríbelo en tu cuaderno de trabajo. Introduce, por ejemplo, en la última escena los coeficientes de las funciones y busca la solución a la preguntas que plantees en dicho enunciado.

Autora: Mª Pilar Arilla Viartola