Área bajo la recta en una representación v/t de un MRUA
La velocidad en un MRUA crece o decrece de forma uniforme con el tiempo. La gráfica velocidad frente a tiempo nos da una recta creciente (si la aceleración es positiva) o decreciente (si la aceleración es negativa).
v(m/s)
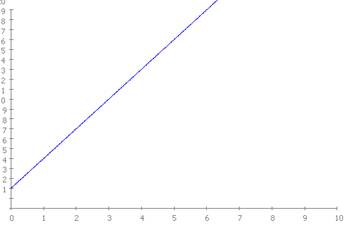 t(s)
t(s)
Vemos que en este movimiento la velocidad inicial es 1 m/s y la aceleración es 3 m/s2.
Si señalamos el área bajo la recta entre dos instantes obtenemos esto:
v(m/s)
 t(s)
t(s)
Entre t = 0 s y t = 2 s,el área bajo la curva se puede calcular mediante el área de un rectángulo y un triángulo.
Del rectángulo es: AR = 2·(2-0) = 4 unidades cuadradas
Del triángulo es : AT =(2-0)·(8-2)/2 = 12/2 = 6 unidades cuadradas
El área total bajo la recta es la suma A total = 4 +6 =10 unidades cuadradas
Comparamos este valor obtenido con el desplazamiento entre t = 0 s y t = 2 s :
s = so + vot + ½ a t2 à Ds = 2(2-0) + ½ 3 (2-0)2 = 4 + 12/2 =10 m
De hecho la ecuación podemos comprobar que surge de hacer esa suma de áreas:
Área del rectángulo : AR = vo·t
Área del triángulo: AT = ½ (v-vo)·t
Si las sumamos,teniendo en cuenta que : v – vo = a·t
Ds = vo·t + ½ ·(v-vo)t = vo·t +1/2 a·t2
La expresión a la que llegamos es: s = so + vo·t +1/2 a·t2
Entra ahora en la página siguiente y observa las gráficas: escena
- La representación es de dos movimientos:uno MRU y uno MRUA
- Distingue cada uno de ellos
- Mueve los controles y realiza las actividades