| |
|
|
|
Situació 1:
Observeu la
següent taula de preus.
| Pes
albergínia (Kg) |
Preu
albergínia(€) |
| 1 |
2,70 |
| 2 |
5,40 |
| 0,5 |
1,35 |
| 10 |
27,00 |
|
 |
De 1 a 2 què han fet, multiplicar o
dividir? i de 2,70 a 5,40?
De 1 a 10 què han fet, multiplicar o dividir? i
de 2,70 a 27,00?
Feu les següents divisions: 2,70/1 5,40/2
1,35/0,5 27/10
Quins són els resultats?
|
Es
diu que dues
magnituds són directament proporcionals si al multiplicar o
dividir una
d'elles per un nombre, l'altra queda multiplicada o dividida pel
mateix nombre.
El quocient entre la segona i la
primera magnitud, s'anomena raó o constant de
proporcionalitat directa. |
|
|
|
Si
multipliquem o dividim les unitats per un nombre, el seu preu queda
multiplicat o dividit pel mateix nombre. I el quocient de les dues
magnituds, la raó, és constant:
Raó=Preu
albergínia/Pes
albergínia=2,70/1=5,40/2=1,35/0,5=27,00/10=2,70€/kg
|
La raó
2,70€/kg expressa el preu de les
albergínies per unitat de pes. Aquesta
raó ens
permet obtenir el preu de les albergínies a partir del pes.
Si volem saber el preu
de 250 grams hem de fer:
0,250kg·2,70€/kg=0,675€
≈ 0,68€.
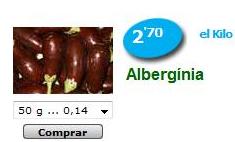
Raona el preu que es
dóna a la imatge per a 50g.
|
Amb
1€ quants quilos d'albergínia podrem comprar?
|
|
Necessitem la raó
inversa.
|
Si la raó
és Preu albergínia/Pes
albergínia=2,70/1, la raó
inversa d'aquesta serà
Pes
albergínia/Preu
albergínia=1/2,70
≈0,37kg/€
Per tant amb un euro
podrem comprar 0,37kg d'albergínies. |
|
Situació
2: Un camió de gelats va a velocitat constant per l'autopista
i en 3
hores
ha fet 240 km. Aleshores com que va sempre a la mateixa velocitat tenim:
| Temps
(hores) |
Distància
recorreguda (km) |
| 3 |
240 |
| 6 |
480 |
| 1'5 |
120 |
| 10 |
800 |
|
 |
|
|
Quina és la raó en
aquest cas?
Raó=Distància
recorreguda/temps =240/3=480/6=120/1,5=800/10=80km/h
La
raó 80km/h expressa la distància recorreguda per
unitat
de temps. Si volem saber quina distància recorre en 9 hores
hem
de fer:
9h·80km/h=720km.
Quant temps
trigarà en recorrer un km?
|
|
|
Una
manera de resoldre activitats de magnituds directament proporcionals
és mitjançant una regla de tres. Però
aquest
procediment es converteix en un mètode que es realitza
de forma completament mecànica, sense saber que
s'està fent.
|
|
|
|
|
La següent escena resol de manera
ordenada
activitats de magnituds directament proporcional sense la
utilització de nombres decimals, reduint a la unitat.
Utilitza-la per resoldre la següent activitat.
Act1: Si 5 kg
de pomes costen 3€, quant costen 2kg? i quants kg puc comprar
amb 7€?
|
|
|
| Un
cop entés el procediement, amb la següent escena es
podran
resoldre activitats de proporcionalitat directa amb qualsevol tipus de
nombres. Utilitza-la per resoldre les activitats de més
avall. |
|
|
|
|
Activitat 2.
Dos quilos
de platans valen 5,5 € , quant
valdran 6,5kg?
Activitat 3.
Volem
preparar una mermelada amb 5kg de maduixes. La recepta
diu
que calen 2kg de sucre per cada 3kg de maduixes. Quina quantitat de
sucre necessitarem nosaltres?
Activitat 4.
Un
cotxe consumeix 56 litres de benzina al recorrer 800 quilòmetres.
Quants litres de benzina consumirà en un viatge de 500 km?
Activitat 5.
Raona quines de les
següents magnituds són directament proporcionals.
| Magnitud
A |
2 |
6 |
8 |
10 |
| Magnitud
B |
3 |
9 |
11 |
20 |
| Magnitud
C |
0,1 |
0,3 |
1,2 |
| Magnitud
D |
2 |
6 |
24 |
|
|
|
|
|
|
|
 Full de treball Full de treball
 Full
de reforç Full
de reforç
 Ampliació Ampliació
|
| |
|