Format
A4 et autres...
Le
format A4
Prenons une feuille de papier
de format A4 classique. Découpons la deux puis en quatre, huit, seize
etc...
Si nous prenons comme unité d'aire celle de la feuille de départ,
nous obtenons des morceaux dont l'aire est 1/2 puis 1/4 puis 1/8, 1/16 1/32
1/64 etc...
Redisposons les morceaux comme indiqué ci-dessous.
En redisposant
correctement les morceaux obtenus, nous pouvons aligner les différents
sommets des rectangles. De même si nous disposons les morceaux au centre
de la feuille initiale, nous constatons que les diagonales des différents
rectangles se superposent. Les sommets des rectangles sont encore alignés
sur les diagonales de la feuille A4 initiale.
Si nous construisons un graphique dont les points ont pour ordonnées
les largeurs des rectangles et pour abscisses leurs longueurs alors ces points
seront alignés sur une droite passant par l'origine identique à
la diagonale commune des rectangles tracée dans l'animation ci-dessus
(fonction linéaire).
Les
morceaux découpés ont tous la même forme.
Le rapport longueur sur largeur est le même pour tous les rectangles
obtenus.
Petite
remarque
Répétons à
l'infini le processus de découpage et calculons la somme des fractions
obtenues avec les aires des différents morceaux
Nous avons une succession de puissances de 1/2. La réunion de tous
les morceaux nous donne la feuille A4 initiale entière. Sur le dessin,
nous constatons donc que la somme infinie des puissances de 1/2 :
1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + ... vaut exactement 1.
Euclide avait pressenti ce résultat et trouvait que la limite de 1/2n
quand n tend vers l'infini est nulle.
Cette notion de limite sera plus clairement définie des siècles
plus tard par Weierstrass en 1865.
On retrouve
le résultat précédent en notant simplement :
S = 1/2 + 1/4
+ 1/8 + 1/16 + 1/32 + ... et encore
S = 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + ... alors
2S = 1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + ... donc
2S = 1 + S ainsi
S = 1
On
peut également utiliser les résultats sur les suites géométriques,
ici nous avons une suite géométrique (chaque terme est
obtenu en multipliant le précédent par 1/2) de raison
1/2 plus petite que 1 et nous pouvons appliquer la formule vraie pour
0<x<1 :
1 + x + x² + x3 +x4 +x5+...
= 1/(1-x)
avec x=1/2 on retrouve
1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + ... = 2
donc
1/2 + 1/4 + 1/8 + 1/16 + 1/32 +... = 1
Autre
format
Prenons une feuille de papier
de format quelconque. Il suffit d'enlever une petite bande d'une feuille ordinaire.
Découpons à nouveau en deux puis en quatre, huit, seize etc...
et adoptons les dispositions déjà vues ci-dessus. Nous n'obtenons
pas les mêmes alignements. En effet cette fois les morceaux obtenus
n'ont pas tous la même forme. Cependant si on observe bien, on peut
noter qu'une fois sur deux, on retrouve certains alignements.
Une
fois sur deux les morceaux découpés ont la même forme.
En
savoir plus
L'Organisation Internationale
de Normalisation (ISO) constitua en 1947 le Comité Technique ISO/TC 6 "papier"
qui chargea un de ses sous-comités d’étudier les dimensions internationales
des papiers et des cartons. La recommandation fut demandée d’envisager la
normalisation des formats.
Comme nous l'avons vu ci-dessus, lorsqu'on plie en deux une feuille A4, le
format reste identique : le rapport longueur sur largeur de la feuille reste
constant. C'est très pratique. Ainsi nous passons du format A3 au format
A4, en pliant des feuilles A3 en deux, puis du format A4 au format A5 en pliant
également en deux une feuille A4.
Comment donc ce résultat a-t-il été obtenu ? Pourquoi
n'est-il pas vrai avec certains autres formats ?
Analysons le format A4
Soit L la longueur d'une feuille et l sa largeur. Lorsqu'on coupe en deux,
la largeur de la nouvelle feuille est L/2 et sa longueur est maintenant
L.
Piour avoir lea même forme il faut que le rapport des deux mesures
soit identique donc que
L/l = l/(L/2) d'où
L²/2 = l² soit
L² = 2 l² ou encore
(L/l)² = 2 et finalement
L/l =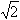 
Le rapport longueur sur largeur est donc d'environ 1,414.
Ainsi pour la largeur de 21 cm la longueur est de 21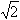
soit d'environ 29,7 cm.
En réalité le point de départ n'est pas la feuille A4
que nous utilisons couramment.
La série principale dérive du format A0 (la série additionnelle repose sur
le même principe à partir de B0, mais le format initial est plus grand).
Nous sommes donc partis de la feuille A0
de même forme mais d'aire 1m² exactement. Elle mesure donc
environ 118,9 cm sur 84,1 cm avec le rapport longueur
sur largeur de .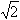
A1 d'aire 1/2 m² mesure environ
84,1 cm sur 59,5 cm.
Le rapport longueur sur largeur est aussi de .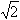
A2
d'aire 1/4 m² mesure environ 59,5 cm sur 42 cm
A3
d'aire 1/8 m² mesure environ 42 cm sur 29,7 cm
A4
d'aire 1/16 m² mesure environ 29,7cm sur 21 cm
A5
d'aire 1/32 m² mesure environ 21cm sur 14,8 cm.
Le rapport Longueur sur largeur est constant c'est toujours .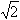
Analysons
les autres formats
Soit L la longueur et
l la largeur (morceau 1).
Après le premier découpage en deux, nous obtenons un morceau
de longueur l et de largeur L/2
qui n'a pas forcément la même forme que le premier.
Ensuite nous obtenons un morceau (morceau 3) de longueur L/2
et de largeur
l/2.
Le rapport longueur /largeur
est le même pour le morceau 1 et pour le morceau 3.
Une fois sur deux les morceaux ont la même forme.
De nombreux autres formats existent.
Ainsi le format 'cloche' correspond à une longueur de 40 cm
pour une largeur de 30 cm ;
le format 'jésus' de 76 cm sur 56 cm ;
le format 'raisin' de 65 cm sur 50 cm ;
le format 'univers' de 130cm sur 100 cm.
PLEIN
ECRAN